1. 下列方程中,一定是关于$x$的一元二次方程的为()
A.$ax^{2}+bx+c = 0$
B.$5x - 2x^{2}+7 = 0$
C.$2y^{2}-x - 3 = 0$
D.$mx^{2}-2x = x^{2}+1$
A.$ax^{2}+bx+c = 0$
B.$5x - 2x^{2}+7 = 0$
C.$2y^{2}-x - 3 = 0$
D.$mx^{2}-2x = x^{2}+1$
答案:
B
2. 用配方法解方程$x^{2}+4x + 1 = 0$时,配方正确的是()
A.$(x - 2)^{2}=5$
B.$(x - 2)^{2}=3$
C.$(x + 2)^{2}=5$
D.$(x + 2)^{2}=3$
A.$(x - 2)^{2}=5$
B.$(x - 2)^{2}=3$
C.$(x + 2)^{2}=5$
D.$(x + 2)^{2}=3$
答案:
D
3. 若$x = 3$是关于$x$的一元二次方程$x^{2}-\frac{5}{3}ax - a^{2}=0(a>0)$的一个根,则下列对$a$的值估计正确的是()
A.$\frac{1}{2}<a<1$
B.$1<a<\frac{3}{2}$
C.$\frac{3}{2}<a<2$
D.$2<a<\frac{5}{2}$
A.$\frac{1}{2}<a<1$
B.$1<a<\frac{3}{2}$
C.$\frac{3}{2}<a<2$
D.$2<a<\frac{5}{2}$
答案:
B
4. 若关于$x$的一元二次方程$x^{2}-4x + c = 0$有两个相等的实数根,则实数$c$的值为()
A.$-16$
B.$-4$
C.$4$
D.$16$
A.$-16$
B.$-4$
C.$4$
D.$16$
答案:
C
5. 小影与小冬一起写作业,解一道一元二次方程时,小影在化简过程中写错了常数项,因而得到方程的两个根是$6$和$1$;小冬在化简过程中写错了一次项的系数,因而得到方程的两个根是$-2$和$-5$。原来的方程可以是()
A.$x^{2}+6x + 5 = 0$
B.$x^{2}-7x + 10 = 0$
C.$x^{2}-5x + 2 = 0$
D.$x^{2}-6x - 10 = 0$
A.$x^{2}+6x + 5 = 0$
B.$x^{2}-7x + 10 = 0$
C.$x^{2}-5x + 2 = 0$
D.$x^{2}-6x - 10 = 0$
答案:
B
6. 已知实数$a$、$b$满足$(a^{2}+b^{2})^{2}-2(a^{2}+b^{2})=8$,则$a^{2}+b^{2}$的值为()
A.$2$
B.$4$
C.$4$或$-2$
D.$-4$或$2$
A.$2$
B.$4$
C.$4$或$-2$
D.$-4$或$2$
答案:
B
7. 已知关于$x$的一元二次方程$x^{2}-mx - n^{2}+mn + 1 = 0$,其中$m$、$n$满足$m - 2n = 3$,关于该方程根的情况,下列判断正确的是()
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.无法确定
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.无法确定
答案:
C
8. 欧几里得的《原本》中记载了形如$x^{2}+ax = b^{2}$的方程的图解法:如图,画$Rt\triangle ABC$,使$\angle ACB = 90^{\circ}$,$BC=\frac{a}{2}$,$AC = b$,再在斜边$AB$上截取$BD=\frac{a}{2}$,则该方程的一个正根是()
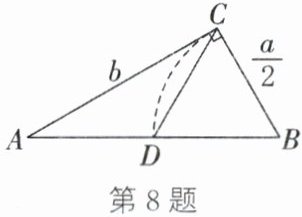
A.$AC$的长
B.$AD$的长
C.$BC$的长
D.$CD$的长

A.$AC$的长
B.$AD$的长
C.$BC$的长
D.$CD$的长
答案:
B
查看更多完整答案,请扫码查看


