《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

1. (2024·聊城)如图,AB、BC、CD是正n边形的三条边,在同一平面内,以BC为边在该正n边形的外部作正方形BCMN.若$∠ABN=120^{\circ }$,则n的值为 ()

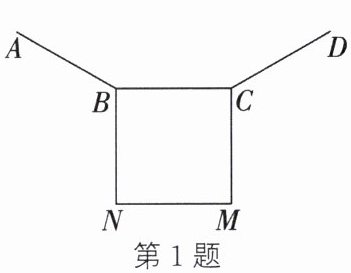
A.12
B.10
C.8
D.6

答案： A

2. (2023·内江)如图,正六边形ABCDEF内接于$\odot O$,点P在$\overset{\frown }{AB}$上,Q是$\overset{\frown }{DE}$的中点,则$∠CPQ$的度数为 ()

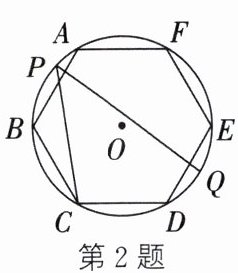
A.$30^{\circ }$
B.$45^{\circ }$
C.$36^{\circ }$
D.$60^{\circ }$

答案： B

3. (新情境·现实生活)(2024·遂宁)佩佩在“黄峨古镇”研学时学习扎染技术,得到一个内角和为1080°的正多边形图案,这个正多边形的每个外角的度数为.

答案： 45°

4. 如图,五边形ABCDE是正五边形.若$l_{1}// l_{2}$,则$∠1-∠2=$°.

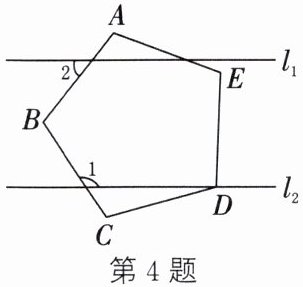
答案： 36

5. (2023·陕西)如图,正八边形的边长为2,对角线AB、CD相交于点E,则BE的长为.

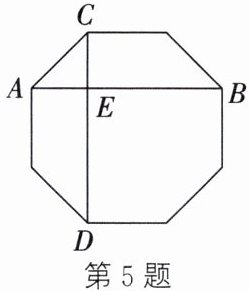
答案： $2\sqrt{2}$

6. 如图,M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
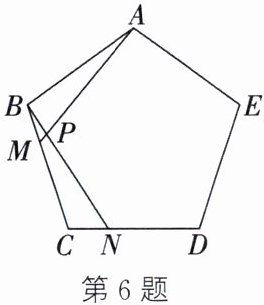
(1) 求证:$\triangle ABM\cong \triangle BCN$;
(2) 求$∠APN$的度数.

答案：
(1)
在正五边形$ABCDE$中，
$AB = BC$，$\angle ABM=\angle BCN$，
在$\triangle ABM$和$\triangle BCN$中，
$\begin{cases}AB = BC\\\angle ABM=\angle BCN\\BM = CN\end{cases}$
根据$SAS$（边角边）判定定理，可得$\triangle ABM\cong\triangle BCN$。
(2)
由$\triangle ABM\cong\triangle BCN$，可得$\angle BAM=\angle CBN$，
因为$\angle APN=\angle BAM+\angle ABP$，
将$\angle BAM=\angle CBN$代入上式得$\angle APN=\angle CBN+\angle ABP$，
而$\angle CBN+\angle ABP=\angle ABC$，
在正五边形$ABCDE$中，$\angle ABC = 108^{\circ}$，
所以$\angle APN = 108^{\circ}$。
综上，答案为：
(1)证明过程如上述；
(2)$\angle APN$的度数为$108^{\circ}$。

7. 如图,设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是 ()

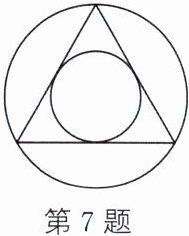
A.$h=R+r$
B.$R=2r$
C.$r=\frac {\sqrt {3}}{4}a$
D.$R=\frac {\sqrt {3}}{3}a$

答案： C