第95页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
23. (新情境·现实生活)为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中各随机抽取10台进行测试,两种电子钟每日的走时误差(单位:s)如下表:

(1)计算甲、乙两种电子钟每日走时误差的平均数.
(2)计算甲、乙两种电子钟每日走时误差的方差.
(3)根据经验,走时稳定性较好的电子钟质量更优.如果这两种电子钟的价格相同,那么你会购买哪种电子钟? 请说明理由.

(1)计算甲、乙两种电子钟每日走时误差的平均数.
(2)计算甲、乙两种电子钟每日走时误差的方差.
(3)根据经验,走时稳定性较好的电子钟质量更优.如果这两种电子钟的价格相同,那么你会购买哪种电子钟? 请说明理由.
答案:
(1) 甲种电子钟每日走时误差的平均数:
$\bar{x}_{甲} = \frac{1 + (-3) + (-4) + 4 + 2 + (-2) + 2 + (-1) + (-1) + 2}{10} = \frac{0}{10} = 0$
乙种电子钟每日走时误差的平均数:
$\bar{x}_{乙} = \frac{4 + (-3) + (-1) + 2 + (-2) + 1 + (-2) + 2 + (-2) + 1}{10} = \frac{0}{10} = 0$
(2) 甲种电子钟每日走时误差的方差:
$s^{2}_{甲} = \frac{(1-0)^{2} + (-3-0)^{2} + (-4-0)^{2} + (4-0)^{2} + (2-0)^{2} + (-2-0)^{2} + (2-0)^{2} + (-1-0)^{2} + (-1-0)^{2} + (2-0)^{2}}{10} = \frac{1 + 9 + 16 + 16 + 4 + 4 + 4 + 1 + 1 + 4}{10} = \frac{60}{10} = 6$
乙种电子钟每日走时误差的方差:
$s^{2}_{乙} = \frac{(4-0)^{2} + (-3-0)^{2} + (-1-0)^{2} + (2-0)^{2} + (-2-0)^{2} + (1-0)^{2} + (-2-0)^{2} + (2-0)^{2} + (-2-0)^{2} + (1-0)^{2}}{10} = \frac{16 + 9 + 1 + 4 + 4 + 1 + 4 + 4 + 4 + 1}{10} = \frac{48}{10} = 4.8$
(3) 购买乙种电子钟。理由:因为 $ s^{2}_{甲} = 6 $,$ s^{2}_{乙} = 4.8 $,且 $ s^{2}_{甲} > s^{2}_{乙} $,所以乙种电子钟走时稳定性更好。
(1) 甲种电子钟每日走时误差的平均数:
$\bar{x}_{甲} = \frac{1 + (-3) + (-4) + 4 + 2 + (-2) + 2 + (-1) + (-1) + 2}{10} = \frac{0}{10} = 0$
乙种电子钟每日走时误差的平均数:
$\bar{x}_{乙} = \frac{4 + (-3) + (-1) + 2 + (-2) + 1 + (-2) + 2 + (-2) + 1}{10} = \frac{0}{10} = 0$
(2) 甲种电子钟每日走时误差的方差:
$s^{2}_{甲} = \frac{(1-0)^{2} + (-3-0)^{2} + (-4-0)^{2} + (4-0)^{2} + (2-0)^{2} + (-2-0)^{2} + (2-0)^{2} + (-1-0)^{2} + (-1-0)^{2} + (2-0)^{2}}{10} = \frac{1 + 9 + 16 + 16 + 4 + 4 + 4 + 1 + 1 + 4}{10} = \frac{60}{10} = 6$
乙种电子钟每日走时误差的方差:
$s^{2}_{乙} = \frac{(4-0)^{2} + (-3-0)^{2} + (-1-0)^{2} + (2-0)^{2} + (-2-0)^{2} + (1-0)^{2} + (-2-0)^{2} + (2-0)^{2} + (-2-0)^{2} + (1-0)^{2}}{10} = \frac{16 + 9 + 1 + 4 + 4 + 1 + 4 + 4 + 4 + 1}{10} = \frac{48}{10} = 4.8$
(3) 购买乙种电子钟。理由:因为 $ s^{2}_{甲} = 6 $,$ s^{2}_{乙} = 4.8 $,且 $ s^{2}_{甲} > s^{2}_{乙} $,所以乙种电子钟走时稳定性更好。
24. 某公司生产A、B两种型号的扫地机器人,为了解它们的扫地质量,工作人员从某月生产的A、B两种型号的扫地机器人中各随机抽取10台,在完全相同的条件下试验,记录下它们的除尘量,并进行整理、描述和分析,制成如下统计表和如图所示的统计图(除尘量用x g表示,共分为三个等级:合格80≤x<85,良好85≤x<95,优秀x≥95),下面给出了部分信息:
10台A型号扫地机器人的除尘量(单位:g):83、84、84、88、89、89、95、95、95、98.
10台B型号扫地机器人中“良好”等级包含的所有数据:85、90、90、90、94.
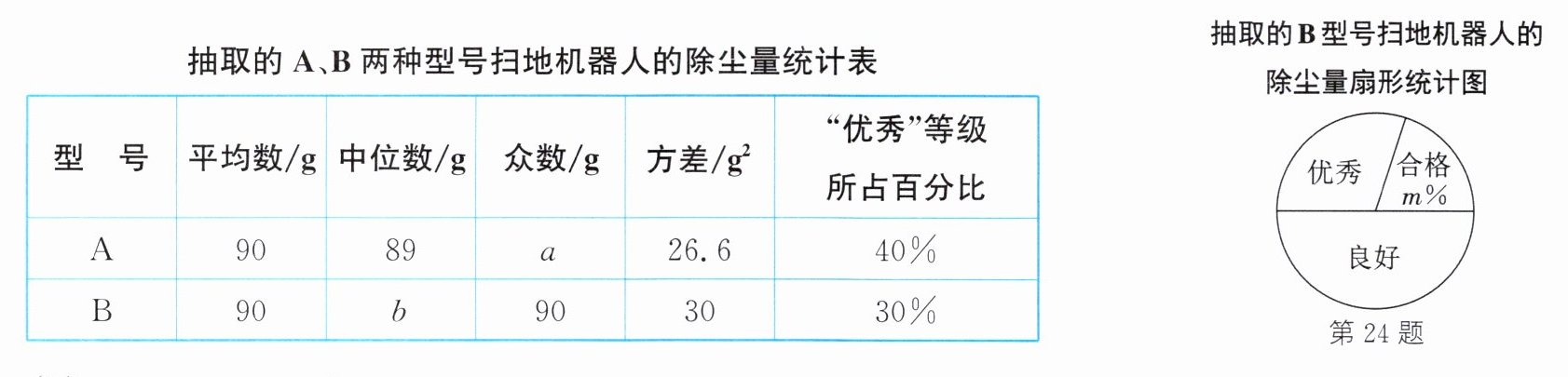
(1)a=,b=,m=.
(2)这个月该公司可生产B型号扫地机器人共3000台,估计该月生产B型号扫地机器人“优秀”等级的台数.
(3)根据以上数据,你认为该公司生产的哪种型号的扫地机器人的扫地质量更好? 请说明理由(写出一条理由即可).
10台A型号扫地机器人的除尘量(单位:g):83、84、84、88、89、89、95、95、95、98.
10台B型号扫地机器人中“良好”等级包含的所有数据:85、90、90、90、94.

(1)a=,b=,m=.
(2)这个月该公司可生产B型号扫地机器人共3000台,估计该月生产B型号扫地机器人“优秀”等级的台数.
(3)根据以上数据,你认为该公司生产的哪种型号的扫地机器人的扫地质量更好? 请说明理由(写出一条理由即可).
答案:
(1)95;90;20
(2)3000×30%=900
答:估计该月生产B型号扫地机器人“优秀”等级的台数为900台。
(3)A型号更好,理由:A型号的方差26.6小于B型号的30,除尘量更稳定。
(1)95;90;20
(2)3000×30%=900
答:估计该月生产B型号扫地机器人“优秀”等级的台数为900台。
(3)A型号更好,理由:A型号的方差26.6小于B型号的30,除尘量更稳定。
查看更多完整答案,请扫码查看


