《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

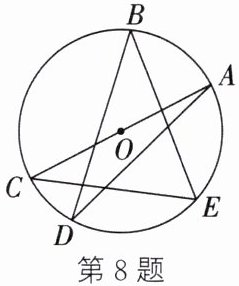
8. (整体思想)如图,点A、B、C、D、E均在$\odot O$上,且AC为$\odot O$的直径,连接AD、CE、BD、BE,则$∠A+∠B+∠C=$$^{\circ}$.

答案： 135

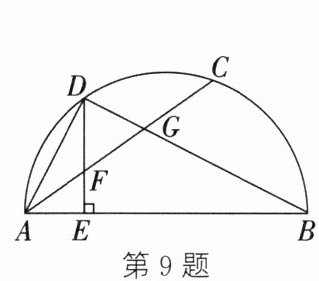
9. (2024·长春)如图,AB是半圆的直径,AC是一条弦,D是$\overset{\frown}{AC}$的中点,$DE⊥AB$于点E,交AC于点F,DB交AC于点G,连接AD.给出下面2个结论:①$∠ABD=∠DAC$;②$AF=FG$.上述结论中,正确结论的序号有.

答案： ①②

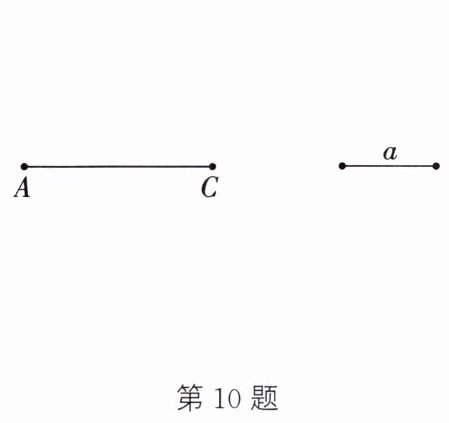
10. 如图,给出线段AC和线段a.
(1) 用直尺和圆规按要求作图(保留作图痕迹,并标明相应的字母,不写作法).
① 作线段AC的垂直平分线l,交线段AC于点O;
② 以线段AC为对角线,作矩形ABCD,使得$AB=a$,且点B在线段AC的上方.
(2) 当$AC=4,a=2$时,(1)中所作矩形ABCD的面积为.

答案：

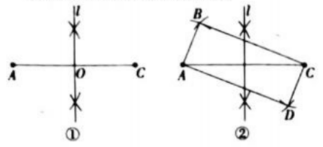
(1)
(2)因为$AC = 4$，$AB = 2$，$AC$为矩形$ABCD$对角线，$\angle ABC=90^{\circ}$。
根据勾股定理$BC=\sqrt{AC^{2}-AB^{2}}=\sqrt{4^{2}-2^{2}} = 2\sqrt{3}$。
矩形$ABCD$的面积$S = AB× BC=2×2\sqrt{3}=4\sqrt{3}$。
故答案为：$4\sqrt{3}$。

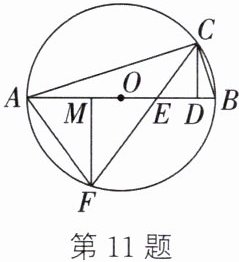
11. (2024·安徽)如图,$\odot O$是$△ABC$的外接圆,D是直径AB上一点,$∠ACD$的平分线交AB于点E,交$\odot O$于另一点F,$FA=FE$.
(1) 求证:$CD⊥AB$;
(2) 若$FM⊥AB$,垂足为M,$OM=OE=1$,求AC的长.

答案：
(1) 连接$OF$，因为$FA = FE$，$OA = OF = OB$（半径），所以$\triangle OFA \cong \triangle OFE$（SSS），则$\angle FOA = \angle FOE$，即$OF$平分$\angle AOE$。设$\angle FOA = \angle FOE = \alpha$，则弧$FA =$弧$FE$，故$\angle FCA = \angle FAE$（等弧所对圆周角相等）。
因为$CF$平分$\angle ACD$，所以$\angle FCA = \angle FCD$，则$\angle FCD = \angle FAE$。
$\angle FEA = \angle FAE$（$FA = FE$），且$\angle FEA$是$\triangle CED$的外角，所以$\angle FEA = \angle FCD + \angle CDE$。
又$\angle ACB = 90°$（直径所对圆周角），即$\angle FCA + \angle FCB = 90°$，而$\angle FCB = \angle FAE$（同弧$FB$所对圆周角），故$\angle FCA + \angle FAE = 90°$。
因为$\angle FCA = \angle FCD$，$\angle FAE = \angle FCD$，所以$\angle FCD + \angle FAE = 90°$，即$\angle CDE = 90°$，因此$CD \perp AB$。
(2) 设$OA = OF = R$（半径），$OM = OE = 1$。在$Rt\triangle OMF$中，$FM^2 = R^2 - 1$；在$Rt\triangle EMF$中，$ME = OM + OE = 2$，$FM^2 = FE^2 - 4$。
因为$FA = FE$，在$Rt\triangle AMF$中，$AM = R - 1$，$FA^2 = (R - 1)^2 + (R^2 - 1) = 2R^2 - 2R$。
由$FE^2 = R^2 + 3$（$FM^2$等量代换），得$2R^2 - 2R = R^2 + 3$，解得$R = 3$（舍负）。
则$AB = 6$，设$AD = x$，由射影定理$AC^2 = AD \cdot AB = 6x$。
$CD \perp AB$，$FM \perp AB$，$\triangle CED \sim \triangle FEM$，$CD = (4 - x)\sqrt{2}$（$AE = 4$）。
在$Rt\triangle ACD$中，$AC^2 = x^2 + [(4 - x)\sqrt{2}]^2$，即$6x = 3x^2 - 16x + 32$，解得$x = 2$（舍$x = \frac{16}{3}$）。
故$AC^2 = 6 × 2 = 12$，$AC = 2\sqrt{3}$。
(1) 证明见解析；
(2) $AC = 2\sqrt{3}$。