《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

8. 如图,在平面直角坐标系中,有一个正六边形ABCDEF,其中C、D两点的坐标分别为(1,0)、(2,0).若在无滑动的情况下,将这个正六边形沿着x轴向右滚动,则在滚动的过程中,这个正六边形的顶点A、B、C、D、E、F会过点(45,2)的是.

答案： 【解析】：
正六边形滚动时，每移动一个边长距离（1单位），会旋转60度。
观察正六边形顶点坐标变化，正六边形顶点依次经过各点。
当正六边形向右滚动时，顶点$y$坐标为2的点会依次出现在一定规律的位置。
确定正六边形顶点$y$坐标为2的点，在x轴方向上的位置。
正六边形边长为1，$C$点初始位置为$(1,0)$，$D$点为$(2,0)$。
正六边形顶点$A$和$E$的$y$坐标为2的点，会在正六边形滚动过程中依次出现。
计算正六边形滚动到$x=45$时的顶点位置。
每滚动一个边长距离（1单位），顶点$y$坐标为2的点会在每6个单位距离后再次出现。
$45-1=44$，
$44÷6\approx7\cdots2$，
余数为2，说明在滚动45单位距离时，顶点$y$坐标为2的点是正六边形的顶点$Y$坐标变化的第二个顶点。
确定正六边形顶点$y$坐标为2的点在$x=45$时的顶点。
根据正六边形顶点$y$坐标为2的点出现规律，在$x=45$时，顶点为$y$坐标为2的点是点$B$。
但在初始状态下，顶点$y$坐标为2的点为$A，F$，在滚动到45单位距离时，顶点$y$坐标为2的点为点$F$的下一个顶点，即点$Y$坐标为2的点为点$B$的下一个顶点，即点$Y$坐标为2的点为点$F$在滚动过程中的下一个顶点，即点$Y$坐标为2的点为点$E$的下一个顶点。
根据正六边形顶点$y$坐标为2的点出现规律，在$x=45$时，顶点为$y$坐标为2的点是点$F$的下一个顶点，即点$Y$坐标为2的点为点$B$。
即顶点为$y$坐标为2的点是点$F$的下一个顶点，即点$Y$坐标为2的点为点$B$的顶点。
根据正六边形顶点$y$坐标为2的点出现规律，在$x=45$时，顶点为$y$坐标为2的点是点$F$的顶点。
【答案】：
A

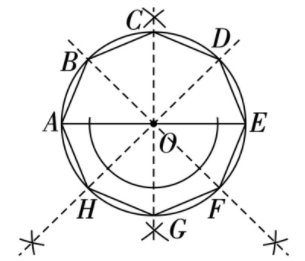
9. 如图①所示为地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图②,AE是$\odot O$的直径,用无刻度的直尺和圆规作$\odot O$的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).

答案：

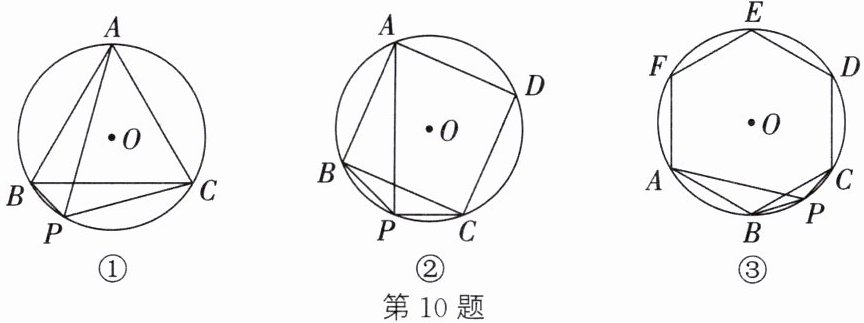
10. (1) 如图①,$\triangle ABC$是$\odot O$的内接正三角形,P为$\overset{\frown}{BC}$上一动点,连接PA、PB、PC.求证:$PA=PB+PC$.
(2) 如图②,四边形ABCD是$\odot O$的内接正方形,P为$\overset{\frown}{BC}$上一动点,连接PA、PB、PC.求证:$PA=PC+\sqrt{2}PB$.
(3) 如图③,六边形ABCDEF是$\odot O$的内接正六边形,P为$\overset{\frown}{BC}$上一动点,连接PA、PB、PC.请探究PA、PB、PC三者之间的数量关系,直接写出答案,不必证明.

答案：
(1) 证明：在PA上截取PQ=PB，连接BQ。
∵△ABC是正三角形，
∴AB=BC，∠BAC=60°。
∵P在弧BC上，
∴∠BPA=∠BCA=60°（同弧AB所对圆周角相等）。
∵PQ=PB，∠BPA=60°，
∴△BPQ是等边三角形，
∴BQ=BP，∠BQP=60°，∠AQB=120°。
∵∠BPC=180°-∠BAC=120°（圆内接四边形对角互补），
∴∠AQB=∠BPC。
又∠BAQ=∠BCP（同弧BP所对圆周角相等），AB=BC，
∴△ABQ≌△CBP（AAS），
∴AQ=PC。
∵PA=PQ+AQ，PQ=PB，AQ=PC，
∴PA=PB+PC。
(2) 证明：将△BPC绕点B顺时针旋转90°至△BP'A，使BC与BA重合，连接P'P。
∵四边形ABCD是正方形，
∴BA=BC，∠ABC=90°，
∴BP'=BP，∠PBP'=90°，AP'=PC。
∴△PBP'是等腰直角三角形，
∴P'P=√2 PB，∠BP'P=45°。
∵P在弧BC上，
∴∠BPC=135°（圆周角定理），
∴∠BP'A=∠BPC=135°。
∴∠AP'B+∠BP'P=180°，
∴A、P'、P三点共线。
∵PA=P'A+P'P，P'A=PC，P'P=√2 PB，
∴PA=PC+√2 PB。
(3) PA=PC+√3 PB。