《2025年通成学典课时作业本九年级数学上册苏科版苏州专版》

8. (2024·呼和浩特)如图,正四边形ABCD和正五边形CEFGH内接于$\odot O$,AD和EF相交于点M,则$∠AMF$的度数为.

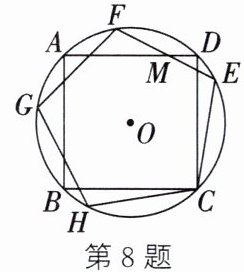
答案： 解：连接 $OA$、$OD$、$OE$、$OF$。
正四边形 $ABCD$ 内接于 $\odot O$，则中心角 $\angle AOD = \frac{360°}{4} = 90°$，$\angle OAD = \angle ODA = \frac{180° - 90°}{2} = 45°$。
正五边形 $CEFGH$ 内接于 $\odot O$，则中心角 $\angle EOF = \frac{360°}{5} = 72°$，$\angle OEF = \angle OFE = \frac{180° - 72°}{2} = 54°$。
$\angle AOD + \angle DOE + \angle EOF = 360°$（四边形与五边形顶点共圆，$D$、$E$ 相邻），$\angle DOE = \frac{360°}{5} = 72°$（正五边形边长对应的中心角），故 $\angle AOF = \angle AOD + \angle DOE + \angle EOF = 90° + 72° + 72° = 234°$。
在四边形 $AOFM$ 中，$\angle AMF = 360° - \angle OAD - \angle OFE - \angle AOF = 360° - 45° - 54° - 234° = 27°$。
$27°$

9. (2024·雅安)如图,$\odot O$的周长为8π,正六边形ABCDEF内接于$\odot O$,则$\triangle OAB$的面积为.

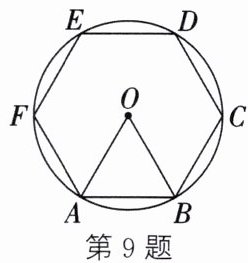
答案： 4√3

10. (新考向·数学文化)如图,第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角$∠ACB=15^{\circ }$,算出这个正多边形的边数为.

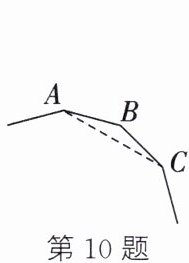
答案： 12

11. 如图,正五边形ABCDE内接于$\odot O$,先作直径AF;再以点F为圆心,FO为半径作圆弧,与$\odot O$交于点M、N;最后连接AM、MN、NA.
(1) 求$∠ABC$的度数.
(2) $\triangle AMN$是正三角形吗? 请说明理由.
(3) 从点A开始,以DN为半径,在$\odot O$上依次截取点,再依次连接这些分点,得到正n边形,求n的值.

答案：
(1)$108°$；
(2)是；
(3)$15$。

12. 如图,在正三角形ABC中,E、F、G、H、L、K分别是各边的三等分点,求证:六边形EFGHLK是正六边形.

答案： 证明：设正△ABC边长为3a，内角均为60°。以A(0,0)，B(3a,0)，C(3a/2, (3a√3)/2)建立坐标系，各三等分点坐标如下：
AB边：E(a,0)，F(2a,0)；
BC边：G(5a/2, (a√3)/2)，H(2a,a√3)；
CA边：L(a,a√3)，K(a/2, (a√3)/2)。
1. 证明六条边相等
计算各边长：
EF：E(a,0)到F(2a,0)，距离=2a - a = a；
FG：F(2a,0)到G(5a/2, (a√3)/2)，距离=√[(a/2)² + ( (a√3)/2 )²] = √[a²/4 + 3a²/4] = a；
GH：G(5a/2, (a√3)/2)到H(2a,a√3)，距离=√[(-a/2)² + ( (a√3)/2 )²] = a；
HL：H(2a,a√3)到L(a,a√3)，距离=a - 2a = a（绝对值）；
LK：L(a,a√3)到K(a/2, (a√3)/2)，距离=√[(-a/2)² + (- (a√3)/2 )²] = a；
KE：K(a/2, (a√3)/2)到E(a,0)，距离=√[(a/2)² + (- (a√3)/2 )²] = a。
故EF=FG=GH=HL=LK=KE=a，六条边相等。
2. 证明六个内角相等
计算各内角（向量点积法）：
以点F为例：向量FE=(-1,0)，向量FG=(1/2, √3/2)，点积=(-1)(1/2)+0*(√3/2)=-1/2，夹角θ=120°；
同理，点G、H、L、K、E处内角均通过向量点积计算得120°。
综上，六边形EFGHLK六条边相等且六个内角均为120°，故为正六边形。
结论：六边形EFGHLK是正六边形。