《2025年名师学案九年级数学下册人教版》

10.（2024·湖北模拟）学生甲在凉亭A处测得湖心岛C在其南偏西15°的方向上，又从A处向正东方向行驶300 m到达凉亭B处，测得湖心岛C在其南偏西60°的方向上，则凉亭B与湖心岛C之间的距离为____m.
　　

答案： $(150 + 150\sqrt{3})$

11. 在Rt△ABC中，∠C = 90°，如果各边都扩大为原来的3倍，则tan A的值 （ ）
A. 不变
B. 扩大为原来的3倍
C. 缩小为原来的$\frac{1}{3}$
D. 不能确定

答案： A

12. AD是△ABC的高，CD = 1，AD = BD = $\sqrt{3}$，则∠BAC的度数为____.

答案： $15^{\circ}$或$75^{\circ}$

13. 在△ABC中，tan A = $\frac{3}{4}$，AB = 5，BC = 4，那么AC的长为____.

答案： $4+\sqrt{7}$或$4-\sqrt{7}$

14.【新课标·数学文化】（2024·资阳）第14届国际数学教育大会（ICME - 14）会标如图1所示，会标中心的图案来源于我国古代数学家赵爽的"弦图"。如图2所示的"弦图"是由四个全等的直角三角形（△ABE，△BCF，△CDG，△DAH）和一个小正方形EFGH拼成的大正方形ABCD。若EF : AH = 1 : 3，则sin∠ABE = （ ）

A. $\frac{\sqrt{5}}{5}$
B. $\frac{3}{5}$
C. $\frac{4}{5}$
D. $\frac{2\sqrt{5}}{5}$

答案： C

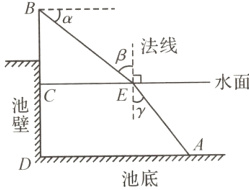
15.【新课标·跨物理学科】（2024·安徽）科技社团选择学校游泳池进行一次光的折射实验，如图，光线自点B处发出，经水面点E折射到池底点A处。已知BE与水平线的夹角α = 36.9°，点B到水面的距离BC = 1.20 m，点A处水深为1.20 m，到池壁的水平距离AD = 2.50 m。点B，C，D在同一条竖直线上，所有点都在同一竖直平面内。记入射角为β，折射角为γ，求$\frac{\sin\beta}{\sin\gamma}$的值（精确到0.1）。（参考数据：sin 36.9°≈0.60，cos 36.9°≈0.80，tan 36.9°≈0.75）

答案： 解：过点E作$EH\perp AD$于点H，由题意可知，$\angle CEB=\alpha = 36.9^{\circ}$，$EH = 1.20$ m，四边形CEHD是矩形，$\therefore CE = DH$。$\therefore CE=\frac{BC}{\tan36.9^{\circ}}\approx\frac{1.20}{0.75}=1.60$(m)，$AH = AD - CE = 2.50 - 1.6 = 0.90$(m)。$\therefore AE=\sqrt{AH^{2}+EH^{2}}=\sqrt{0.90^{2}+1.20^{2}} = 1.50$(m)，$\sin\gamma=\frac{AH}{AE}=\frac{0.90}{1.50}=0.60$。$\because\sin\beta=\sin\angle CBE=\frac{CE}{BE}=\cos\angle CEB=\cos\alpha = 0.80$，$\therefore\frac{\sin\beta}{\sin\gamma}=\frac{0.80}{0.60}\approx1.3$。