第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
活动一:在学习了相似三角形的应用后,同学们一定掌握了不少测量旗杆高度的方法。请阅读下面两个素材:
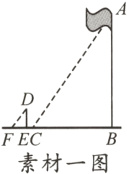
素材一:在某一时刻,借助太阳光线,测得小华的身高DE为1.8m,他的影长EF为0.9m,同时测得旗杆AB的影长BC为6m。
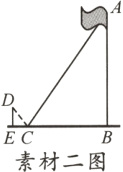
素材二:利用“光在反射时,反射角等于入射角”的规律,小丽在她的脚下C点放了一面小镜子,然后向后退1.2m到达点E,恰好在小镜子中看到旗杆的顶端A,此时旗杆底端B到点C的距离BC为9m,小丽的眼睛点D到地面的距离DE为1.6m。
任务1:请计算素材一中旗杆的高度;
任务2:请计算素材二中旗杆的高度。
素材一:在某一时刻,借助太阳光线,测得小华的身高DE为1.8m,他的影长EF为0.9m,同时测得旗杆AB的影长BC为6m。

素材二:利用“光在反射时,反射角等于入射角”的规律,小丽在她的脚下C点放了一面小镜子,然后向后退1.2m到达点E,恰好在小镜子中看到旗杆的顶端A,此时旗杆底端B到点C的距离BC为9m,小丽的眼睛点D到地面的距离DE为1.6m。

任务1:请计算素材一中旗杆的高度;
任务2:请计算素材二中旗杆的高度。
答案:
解:任务1:由题意,得∠DEF = ∠ABC = 90°,DF//AC,
∴∠DFE = ∠ACB.
∴△DEF∽△ABC.
∴$\frac{DE}{AB}=\frac{EF}{BC}$.
∴$\frac{1.8}{AB}=\frac{0.9}{6}$. 解得AB = 12. 答:旗杆高度为12 m;
任务2:由题意,得∠DEC = ∠ABC = 90°,∠DCE = ∠ACB,
∴△DEC∽△ABC.
∴$\frac{DE}{AB}=\frac{EC}{BC}$.
∴$\frac{1.6}{AB}=\frac{1.2}{9}$. 解得AB = 12. 答:旗杆高度为12 m.
∴∠DFE = ∠ACB.
∴△DEF∽△ABC.
∴$\frac{DE}{AB}=\frac{EF}{BC}$.
∴$\frac{1.8}{AB}=\frac{0.9}{6}$. 解得AB = 12. 答:旗杆高度为12 m;
任务2:由题意,得∠DEC = ∠ABC = 90°,∠DCE = ∠ACB,
∴△DEC∽△ABC.
∴$\frac{DE}{AB}=\frac{EC}{BC}$.
∴$\frac{1.6}{AB}=\frac{1.2}{9}$. 解得AB = 12. 答:旗杆高度为12 m.
活动二:请根据教材P54活动1的第2个图与同学合作,设计出一种新的测量方法,写出你的测量方案,并计算出旗杆的高度。
答案:
活动二:解:答案不唯一,方法如下:
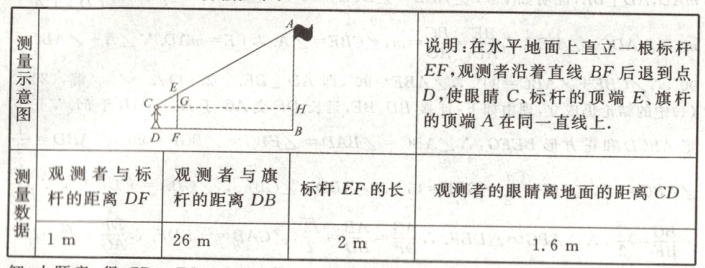
解:由题意,得CD = FG = BH = 1.6 m,CG = DF = 1 m,CH = BD = 26 m,∠CGE = ∠CHA = 90°,
∵EF = 2 m,
∴EG = EF - FG = 2 - 1.6 = 0.4(m).
∵∠ECG = ∠ACH,∠AHC = ∠EGC = 90°,
∴△ECG∽△ACH.
∴$\frac{CG}{CH}=\frac{EG}{AH}$,即$\frac{1}{26}=\frac{0.4}{AH}$,解得AH = 10.4.
∴AB = AH + BH = 10.4 + 1.6 = 12(m),答:旗杆AB的高度为12 m.
活动二:解:答案不唯一,方法如下:

解:由题意,得CD = FG = BH = 1.6 m,CG = DF = 1 m,CH = BD = 26 m,∠CGE = ∠CHA = 90°,
∵EF = 2 m,
∴EG = EF - FG = 2 - 1.6 = 0.4(m).
∵∠ECG = ∠ACH,∠AHC = ∠EGC = 90°,
∴△ECG∽△ACH.
∴$\frac{CG}{CH}=\frac{EG}{AH}$,即$\frac{1}{26}=\frac{0.4}{AH}$,解得AH = 10.4.
∴AB = AH + BH = 10.4 + 1.6 = 12(m),答:旗杆AB的高度为12 m.
查看更多完整答案,请扫码查看


