《2025年名师学案九年级数学下册人教版》

15.将一张以AB为边的矩形纸片，先沿一条直线剪掉一个直角三角形，在剩下的纸片中，再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似)，剩下的是如图所示的四边形纸片ABCD，其中∠A = 90°，AB = 9，BC = 7，CD = 6，AD = 2，则剪掉的两个直角三角形的斜边长不可能是（ ）
　
　
A.$\frac{25}{2}$ B.$\frac{45}{4}$ C.10 D.$\frac{35}{4}$　　

答案： A

16.如图，在等腰三角形ABC中，AB = AC = 8，BC = 6，将△ABC的一角沿着MN折叠，使点B与点B'重合，且点B'落在AC上。若△ABC与△B'MC相似，则BM的长度为______。
　　

答案： 3或$\frac{27}{4}$

17.如图，△ABO的顶点A在函数y = $\frac{k}{x}$(x ＞ 0)的图象上，∠ABO = 90°，过AO边的三等分点M，N分别作x轴的平行线交AB于点P，Q。若四边形MNQP的面积为3，则k的值为（ ）
　　
A.9 B.12 C.15 D.18

答案： D

18.【新课标·跨语文学科】(2024·山西)黄金分割是汉字结构最基本的规律。借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观。已知一条分割线的端点A，B分别在习字格的边MN，PQ上，且AB//NP，“晋”字的笔画“、”的位置在AB的黄金分割点C处，且$\frac{BC}{AB}$ = $\frac{\sqrt{5}−1}{2}$，若NP = 2 cm。则BC的长为__________cm(结果保留根号)。
　　

答案： ($\sqrt{5}$ - 1)

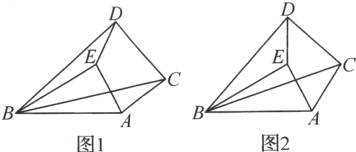
19.如图1，已知线段AB，AC，线段AC绕点A在直线AB上方旋转，连接BC，以BC为边在BC上方作Rt△BDC，且∠BDC = 90°，∠DBC = 30°，以AB为边在AB上方作Rt△BAE，且∠AEB = 90°，∠EBA = 30°，连接DE。
　　(1)求线段DE与AC的数量关系；
　　(2)如图2，若DE⊥AB，AB = 4，AC = 2，求BC的长。
　　　　

答案： 解：
(1)在Rt△BDC中，∠DBC = 30°，在Rt△BAE中，∠AEB = 90°，∠EBA = 30° = ∠DBC，
∴∠DBE = ∠ABC，
∴△ABE∽△CBD，
∴$\frac{AB}{BE}$ = $\frac{BC}{BD}$，即$\frac{AB}{BE}$ = $\frac{BC}{BD}$.又
∵∠DBE = ∠ABC，
∴△ABC∽△EBD，
∴$\frac{BE}{AB}$ = $\frac{DE}{AC}$，在Rt△ABE中，∠AEB = 90°，∠ABE = 30°，
∴AE = $\frac{1}{2}$AB，
∴BE = $\frac{\sqrt{3}}{2}$AB，即$\frac{BE}{AB}$ = $\frac{\sqrt{3}}{2}$，
∴$\frac{DE}{AC}$ = $\frac{BE}{AB}$ = $\frac{\sqrt{3}}{2}$，即DE = $\frac{\sqrt{3}}{2}$AC；
(2)延长DE交BA于F，由
(1)知AE = $\frac{1}{2}$AB = 2，∠BAE = 60°，在Rt△AEF中，∠AEF = 30°，
∴AF = $\frac{1}{2}$AE = 1，EF = $\sqrt{2² - 1²}$ = $\sqrt{3}$，
∴BF = AB - AF = 3，由
(1)知DE = $\frac{\sqrt{3}}{2}$AC = $\frac{\sqrt{3}}{2}$×2 = $\sqrt{3}$，
∴DF = DE + EF = 2$\sqrt{3}$，在Rt△BDF中，DB = $\sqrt{BF² + DF²}$ = $\sqrt{3² + (2\sqrt{3})²}$ = $\sqrt{21}$.
∵△ABC∽△EBD，
∴$\frac{BC}{BD}$ = $\frac{AC}{ED}$，即$\frac{BC}{\sqrt{21}}$ = $\frac{2}{\sqrt{3}}$，
∴BC = 2$\sqrt{7}$.