《2025年名师学案九年级数学下册人教版》

12.如果在△ABC中，$\sin A = \cos B = \frac{\sqrt{2}}{2}$，那么下列最确切的结论是（ ）
A.△ABC是直角三角形
B.△ABC是等腰三角形
C.△ABC是等腰直角三角形
D.△ABC是锐角三角形

答案： C

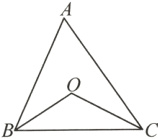
13.如图，点O在△ABC内，且到三边的距离相等，若∠BOC = 120°，则sin A的值为（ ）

A.$\sqrt{3}$
B.$\frac{\sqrt{3}}{3}$
C.$\frac{\sqrt{3}}{2}$
D.$\frac{\sqrt{2}}{2}$

答案： C

14.α，β满足0°＜α＜β＜45°，下列关于α，β的命题错误的是（ ）
A.$0＜\sin\alpha＜\frac{\sqrt{2}}{2}$
B.$0＜\tan\beta＜1$
C.$\cos\beta＜\sin\alpha$
D.$\sin\beta＜\cos\alpha$

答案： C

15.正比例函数$y = \sqrt{3}x$的图象与x轴的夹角为锐角α，则α=_______.

答案： 60°

16.计算：$\sqrt{12}-2\cos30^{\circ}+|\sqrt{3}-2|+2^{-1}+\sqrt{3}\tan30^{\circ}$.

答案： 解：原式=$2\sqrt{3}-2\times\frac{\sqrt{3}}{2}+2-\sqrt{3}+\frac{1}{2}+\sqrt{3}\times\frac{\sqrt{3}}{3}=3\frac{1}{2}$.

17.【一日一优】【新中考·解题方法型阅读理解题】数形结合思想是通过构造几何图形来解决代数问题的重要思想.通过这一节的学习，我们已经知道30°，45°，60°角的正切值，小明同学对计算tan 22.5°产生兴趣，进行了以下探究.
（1）构造图形：如图，在Rt△ABC中，∠C = 90°，∠ABC = 45°，延长CB至点D，使BD = AB，连接AD，求tan D的值.

解：设AC = x，则BC = x，
BD = AB，∠ABC = 45°，
请你将解题过程补充完整；
（2）类比推理：
请你仿照上面的思路，构造图形，计算tan 75°的值.

答案：
解：
(1)
∵BD = AB，∠ABC = 45°，
∴∠D = ∠BAD = 22. 5°.
∵AB = $\sqrt{x^{2}+x^{2}}=\sqrt{2}x$，
∴BD = AB = $\sqrt{2}x$.
∴tan D=$\frac{AC}{CD}=\frac{x}{\sqrt{2}x + x}=\sqrt{2}-1$；
(2)如图，Rt△ABC 中，∠C = 90°，∠ABC = 30°，延长 CB 至 D，使 BD = AB. 设 AC = x，则 AB = BD = 2x，BC = $\sqrt{3}x$.
∵AB = BD，∠ABC = 30°，
∴∠D = ∠DAB = 15°.
∴∠DAC = 75°. tan 75° = tan∠DAC = $\frac{DC}{AC}=\frac{2x+\sqrt{3}x}{x}=2+\sqrt{3}$.