《2025年名师学案九年级数学下册人教版》

1.【变式1:改变条件,截两个正方形】
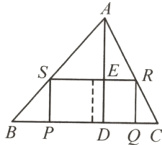
如图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC = 80,AD = 60,四边形PQRS是由两个并排放置的正方形所组成的矩形,则矩形的边PQ的长为多少?

答案： 解:设小正方形边长为x，由题意，得$SP = ED = x,AE = 60 - x,SR = 2x,SR// PQ$，$\angle ADB = 90^{\circ}$。$\therefore \triangle ASR\backsim\triangle ABC$，$\angle AES=\angle ADB = 90^{\circ}$，$\therefore\frac{AE}{AD}=\frac{SR}{BC}$。即$\frac{60 - x}{60}=\frac{2x}{80}$，解得$x = 24$。$\therefore PQ = SR = 2x = 48$。答:矩形的边PQ的长为48。

2.【变式2:改变条件和问题】
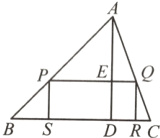
如图,在△ABC内截一个矩形,且一边落在BC边上,另两个顶点分别在边AB,AC上,AD⊥BC于点D,BC = 80,AD = 60,求矩形PQRS面积的最大值.

答案： 解:设$PQ = x$。$\because AD\perp BC$，$\therefore\angle ADB = 90^{\circ}$。$\because$矩形PQRS，$\therefore PQ// BC$。$\therefore\triangle APQ\backsim\triangle ABC$，$\angle AEP=\angle ADB = 90^{\circ}$。$\therefore\frac{AE}{AD}=\frac{PQ}{BC}$，即$\frac{AE}{60}=\frac{x}{80}$。$\therefore AE=\frac{3}{4}x$，$\therefore ED = AD - AE = 60-\frac{3}{4}x = PS$。$\therefore S_{矩形PQRS}=x(60 - \frac{3}{4}x)=-\frac{3}{4}x^{2}+60x(0 ＜ x ＜ 80)$。$\because-\frac{3}{4}＜0$，开口向下，$\therefore$当$x = -\frac{60}{2\times(-\frac{3}{4})}=40$时，矩形PQRS的面积最大，最大值是1200。

3.【变式3:改变截取方法】
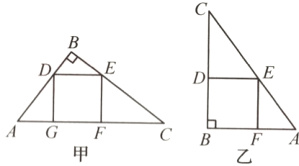
一块直角三角形木板的面积为1.5 m²,其中一条直角边AB为1.5 m,怎样才能把它加工成一个无拼接且面积最大的正方形桌面?甲、乙两位木匠的加工方法如图所示,请你用学过的知识说明哪位木匠的方法符合要求(加工损耗不计,计算结果中的分数可保留).

答案： 解:由$AB = 1.5m$，$S_{\triangle ABC}=1.5m^{2}$，可得$BC = 2m$。甲:过点B作$BH\perp AC$于点H，交DE于点P。$\because AB = 1.5m$，$BC = 2m$，$\therefore AC=\sqrt{AB^{2}+BC^{2}} = 2.5m$。由$S_{\triangle ABC}=\frac{1}{2}AC\cdot BH=\frac{1}{2}AB\cdot BC$，得$BH=\frac{AB\cdot BC}{AC}=1.2m$。设甲设计的正方形桌面的边长为x m，$\because DE// AC$，$\therefore Rt\triangle BDE\backsim Rt\triangle BAC$。$\therefore\frac{BP}{BH}=\frac{DE}{AC}$，即$\frac{1.2 - x}{1.2}=\frac{x}{2.5}$，解得$x=\frac{30}{37}$。设乙设计的正方形桌面的边长为y m，由$DE// AB$，得$Rt\triangle CDE\backsim Rt\triangle CBA$。$\therefore\frac{DE}{BA}=\frac{CD}{CB}$，即$\frac{y}{1.5}=\frac{2 - y}{2}$，解得$y=\frac{6}{7}$。$\because 0 ＜ x ＜ y$，$\therefore x^{2}＜y^{2}$，即$S_{正方形甲}＜S_{正方形乙}$。$\therefore$乙木匠的方法符合要求。