第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
11.(2024·湖北节选)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H。
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB = 2,AD = 3时,求GH的长。
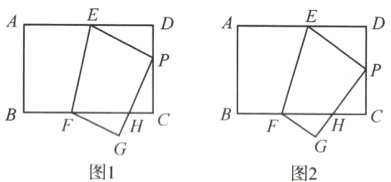
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB = 2,AD = 3时,求GH的长。

答案:
(1)证明:
∵矩形ABCD,
∴∠A = ∠D = ∠C = 90°.
∴∠DEP + ∠EPD = 90°.
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH = ∠A = 90°.
∴∠EPD + ∠CPH = 90°.
∴∠DEP = ∠CPH.又
∵∠D = ∠C,
∴△EDP∽△PCH;
(2)解:
∵四边形ABCD是矩形,
∴CD = AB = 2,AD = BC = 3,∠A = ∠D = ∠C = 90°.
∵P为CD中点,
∴DP = CP = $\frac{1}{2}$×2 = 1.设EP = AE = x,则ED = AD - x = 3 - x.在Rt△EDP中,EP² = ED² + DP²,即x² = (3 - x)² + 1,解得x = $\frac{5}{3}$.
∴EP = AE = x = $\frac{5}{3}$.
∴ED = AD - AE = $\frac{4}{3}$.
∵△EDP∽△PCH,
∴$\frac{ED}{PC}$ = $\frac{EP}{PH}$,即$\frac{\frac{4}{3}}{1}$ = $\frac{\frac{5}{3}}{PH}$.
∴PH = $\frac{5}{4}$.
∵PG = AB = 2,
∴GH = PG - PH = $\frac{3}{4}$.
(1)证明:
∵矩形ABCD,
∴∠A = ∠D = ∠C = 90°.
∴∠DEP + ∠EPD = 90°.
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH = ∠A = 90°.
∴∠EPD + ∠CPH = 90°.
∴∠DEP = ∠CPH.又
∵∠D = ∠C,
∴△EDP∽△PCH;
(2)解:
∵四边形ABCD是矩形,
∴CD = AB = 2,AD = BC = 3,∠A = ∠D = ∠C = 90°.
∵P为CD中点,
∴DP = CP = $\frac{1}{2}$×2 = 1.设EP = AE = x,则ED = AD - x = 3 - x.在Rt△EDP中,EP² = ED² + DP²,即x² = (3 - x)² + 1,解得x = $\frac{5}{3}$.
∴EP = AE = x = $\frac{5}{3}$.
∴ED = AD - AE = $\frac{4}{3}$.
∵△EDP∽△PCH,
∴$\frac{ED}{PC}$ = $\frac{EP}{PH}$,即$\frac{\frac{4}{3}}{1}$ = $\frac{\frac{5}{3}}{PH}$.
∴PH = $\frac{5}{4}$.
∵PG = AB = 2,
∴GH = PG - PH = $\frac{3}{4}$.
12.【新课标·综合与实践】如图,昌昌同学和同伴秋游时,发现在某小山坡的点E处有一棵小树,他们想利用皮尺、测倾器和平面镜测量小树到山脚的距离(即DE的长度),昌昌站在点B处,让同伴移动平面镜至点C处,此时昌昌在平面镜内刚好可以看到点E,且测得BC = 4.8 m,CD = 28 m,∠CDE = 135°,已知昌昌的眼睛到地面的距离AB = 1.6 m,请根据以上数据,求DE的长度。(结果保留根号)
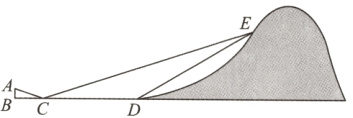

答案:
解:过点E作EF⊥BD,交BD延长线于点F,则∠EDF = 180° - 135° = 45°,设DF = x m = EF,由题意知∠B = ∠EFC = 90°,∠ACB = ∠ECF,
∴△ABC∽△EFC.
∴$\frac{AB}{EF}$ = $\frac{BC}{CF}$,即$\frac{1.6}{x}$ = $\frac{4.8}{28 + x}$.解得x = 14.经检验,x = 14是原方程的解.
∴DF = EF = 14.
∴DE = $\sqrt{14² + 14²}$ = 14$\sqrt{2}$.答:DE的长为14$\sqrt{2}$ m.
∴△ABC∽△EFC.
∴$\frac{AB}{EF}$ = $\frac{BC}{CF}$,即$\frac{1.6}{x}$ = $\frac{4.8}{28 + x}$.解得x = 14.经检验,x = 14是原方程的解.
∴DF = EF = 14.
∴DE = $\sqrt{14² + 14²}$ = 14$\sqrt{2}$.答:DE的长为14$\sqrt{2}$ m.
13.如图,四边形ABCD与四边形A'B'C'D'位似,点O是它们的位似中心,若OA : OA' = 2 : 3,则CD : C'D'的值为( )
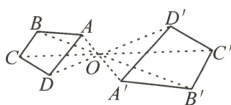
A.$\frac{1}{2}$
B.$\frac{2}{3}$
C.$\frac{2}{5}$
D.$\frac{4}{9}$

A.$\frac{1}{2}$
B.$\frac{2}{3}$
C.$\frac{2}{5}$
D.$\frac{4}{9}$
答案:
B
14.在平面直角坐标系中,以原点O为位似中心,作△ABC的位似图形△A'B'C',△ABC与△A'B'C'的相似比为1 : 2,若点A的坐标为(2,3),则点A'的坐标为______。
答案:
(4,6)或(-4,-6)
查看更多完整答案,请扫码查看


