《2025年名师学案九年级数学下册人教版》

9.【分类讨论思想】如图，

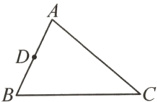
$\triangle ABC$中，$AB = 3$，$AC = 4$，$D$是$AB$的中点，在边$AC$上确定点$E$的位置，使得$\triangle ADE$与$\triangle ACB$相似，则$AE$的长为________.
【点拨】用“与”或“和”表示的两个相似三角形，由于对应关系不明确，需要分类讨论.

答案： $\frac{9}{8}$或2

10. 在三角形纸片$ABC$中，$AB = 8$，$BC = 4$，$AC = 6$，按下列方法沿虚线剪下，能使阴影部分的三角形与$\triangle ABC$相似的是（ ）

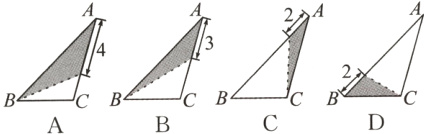
答案： D

11. 在如图所示的象棋棋盘（各个小正方形的边长均相等）中，根据“马走日”的规则，“马”应落在下列哪个位置处，能使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似（ ）

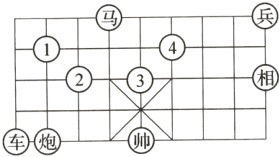
A. ①处
B. ②处
C. ③处
D. ④处

答案： B

12.【分类讨论思想】如图，在平面直角坐标系中，已知点$A(2,0)$，$B(0,4)$，在$x$轴上找到点$C(1,0)$和$y$轴的正半轴上找到点$D$，使$\triangle AOB$与$\triangle DOC$相似，则$D$点的坐标是______.

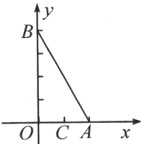
答案： $(0,\frac{1}{2})$或(0,2)

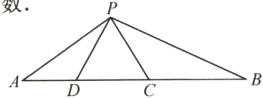
13. 如图，点$C$，$D$在线段$AB$上，$\triangle PCD$是等边三角形，且$CD^{2}=AD\cdot BC$.
(1)求证：$\triangle APD\sim\triangle PBC$；
(2)求$\angle APB$的度数.

答案：
(1)证明：
∵△PCD是等边三角形，
∴PD = PC = DC，∠PDC = ∠PCD = 60°.
∴∠ADP = ∠PCB = 120°.
∵CD² = AD·BC，
∴AD : PC = PD : BC.
∴△APD∽△PBC.
(2)解：
∵△APD∽△PBC，
∴∠APD = ∠B.
∵∠B + ∠BPC = ∠PCD = 60°，
∴∠APD + ∠BPC = 60°.
∴∠APB = 60° + ∠DPC = 120°.

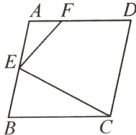
14.【一日一优】如图，菱形$ABCD$中，$E$是边$AB$的中点，$F$是边$AD$上一点，连接$CE$，$EF$. 若$AE = 3$，$EF = 2AF = 4$，求$CE$的长.

答案： 解：延长FE交CB的延长线于M.
∵四边形ABCD是菱形，
∴AD//BC，AB = BC.
∵E是边AB的中点，
∴AE = BE，
∴△AEF≌△BEM(AAS).
∴∠AFE = ∠M，∠A = ∠EBM.
∵AE = 3，EF = 2AF = 4，
∴ME = 4，BM = 2，BE = 3.
∴BC = AB = 2AE = 6.
∴MC = 8，
∴$\frac{MB}{ME}=\frac{2}{4}=\frac{1}{2}$，$\frac{ME}{MC}=\frac{4}{8}=\frac{1}{2}$，
∴$\frac{MB}{ME}=\frac{ME}{MC}$.
∵∠M = ∠M，
∴△MEB∽△MCE.
∴$\frac{BE}{EC}=\frac{MB}{ME}=\frac{1}{2}$.
∵BE = 3，
∴CE = 6.