《2025年名师学案九年级数学下册人教版》

8.【教材P92练习变式】如图，箭头表示投影方向，画出下列图形的正投影.

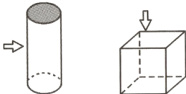
答案：
解：如图所示。

9.【教材P92习题T1变式】下面是一天中四个不同时刻两座建筑物的影子，将它们按时间先后顺序排列正确的是( )

A. (3)(1)(4)(2) B. (3)(2)(1)(4)
C. (3)(4)(1)(2) D. (2)(4)(1)(3)

答案： C

10. 如图，长方体的一个底面ABCD在投影面P上，M，N分别是侧棱BF，CG的中点，矩形EFGH与矩形EMNH在投影面P上的正投影都是矩形ABCD，设它们的面积分别是S₁，S₂，S，则S₁，S₂，S的大小关系是______(用“＝”“＞”或“＜”连接).

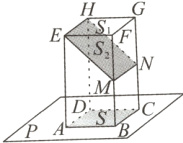
答案： $S_{1}=S＜S_{2}$

11. 如图，在水平地面上竖立着一面墙AB，墙外有一盏路灯D. 光线DC恰好通过墙的最高点B，且与地面形成37°角. 墙在灯光下的影子为线段AC，并测得AC＝5.5 m.

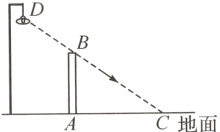
(1)则墙AB的高度约是______m；(结果精确到0.1 m. 参考数据：tan 37°≈0.75，sin 37°≈0.60，cos 37°≈0.80)
(2)如果要缩短影子AC的长度，同时不能改变墙的高度和位置，请你写出两种不同的方法.

答案：
(1)4.1 解：
(2)方法1：增加路灯D的高度；方法2：使路灯D向墙靠近。

12.【一日一优】为测量图①和图②中的树高，在同一时刻，某小组学生分别作了如下操作：如图①，测得竹竿CD的长为0.8 m，其阳光下的影长CE为1 m，以及图①中树影长AE为2.4 m；如图②，测量落在地面上的树影长2.8 m，测量在墙上的树影高1.2 m. 请问图①与图②中的树高分别是多少？

答案：
解：由题意可知，$\frac{AB}{AE}=\frac{CD}{CE}$，即$\frac{AB}{2.4}=\frac{0.8}{1}$，解得$AB = 1.92m$；设图②中的树高为$x m$，则$FM=(x - 1.2)m$，由题意知，$\frac{FG}{MF}=\frac{CE}{DC}$，即$\frac{2.8}{x - 1.2}=\frac{1}{0.8}$，解得$x = 3.44$。答：图①中的树高1.92m，图②中的树高3.44m。