《2025年名师学案九年级数学下册人教版》

6.（2024·盐城）如图，小明用无人机测量教学楼的高度，将无人机垂直上升距地面30 m的点P处，测得教学楼底端点A的俯角为37°，再将无人机沿教学楼方向水平飞行26.6 m至点Q处，测得教学楼顶端点B的俯角为45°，则教学楼AB的高度约为______m。（精确到1 m，参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75）
　　　　　

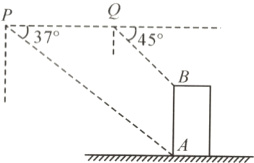
答案： 17

7. 图1是某款笔记本电脑的支架，它可以进行角度调节，图2是它的平面示意图。已知AO = OB = 22 cm，当∠AOB = 123°，∠B = 15°时，用眼舒适度较为理想，求此时顶部边缘A处离桌面BC的高度。（结果精确到1 cm，参考数据：sin 18°≈0.31，cos 18°≈0.95，tan 18°≈0.32，sin 15°≈0.26，cos 15°≈0.97，tan 15°≈0.27）
　　　　　

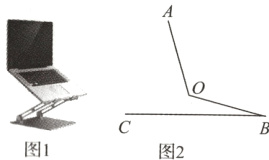
答案： 解：过点$A$作$AE\perp BC$于点$E$，过点$O$分别作$OD\perp BC$于点$D$，$OF\perp AE$于点$F$，则四边形$ODEF$为矩形，$\therefore OD = FE,\angle FOD = 90^{\circ}$. 在$Rt\triangle BOD$中，$\angle B = 15^{\circ},OB = 22cm,\therefore OD = OB\cdot\sin B\approx22\times0.26 = 5.72(cm)$. 在$Rt\triangle AOF$中，$\angle AOF = 360^{\circ}-123^{\circ}-(90^{\circ}-15^{\circ})-90^{\circ}=72^{\circ},\therefore\angle A = 90^{\circ}-72^{\circ}=18^{\circ}.\because OA = 22cm,\therefore AF = OA\cdot\cos A\approx22\times0.95 = 20.9(cm).\therefore AE = AF + FE = AF + OD = 20.9 + 5.72\approx27(cm)$. 答：顶部边缘$A$处离桌面$BC$的高度约为$27cm$.

8.【一日一优】【新情境·安全出行】超速容易造成交通事故，高速公路管理部门在某隧道内的C，E两处安装了测速仪，该段隧道的截面示意图如图所示，图中所有点都在同一平面内，且A，D，B，F在同一直线上。点C，E到AB的距离分别为CD，EF，且CD = EF = 7 m，CE = 895 m，在C处测得A点的俯角为30°，在E处测得B点的俯角为45°，小型汽车从点A行驶到点B所用时间为45 s。
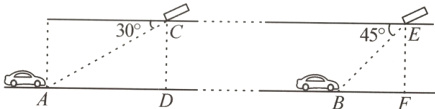
（1）求A，B两点之间的距离（结果精确到1 m）；
（2）若该隧道限速80千米/小时，判断小型汽车从点A行驶到点B是否超速？并通过计算说明理由。（参考数据：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7）
　

答案： 解：
(1)根据题意，四边形$CDFE$是矩形，$\angle CAD = 30^{\circ},\angle EBF = 45^{\circ},DF = CE = 895m$. 在$Rt\triangle EBF$中，$BF=\frac{EF}{\tan\angle EBF}=\frac{7}{1}=7(m).\therefore DB = DF - BF = 895 - 7 = 888(m)$. 在$Rt\triangle ACD$中，$AD=\frac{CD}{\tan\angle CAD}=7\sqrt{3}\approx11.9(m).\therefore AB = AD + BD = 11.9 + 888\approx900(m)$. 答：$A,B$两点之间的距离为$900m$；
(2)$\because900\div45 = 20(m/s),\therefore$小型汽车每小时行驶$20\times3600 = 72000(m),\because72000m = 72km,72\lt80,\therefore$小型汽车从点$A$行驶到点$B$没有超速.