《2025年名师学案九年级数学下册人教版》

如图，我们通常把坡面的______高度h和______宽度l的比叫做坡度（或坡比），一般用字母i表示，即i = tanα = ______．这里，α是______与______的夹角，这个角叫做坡角。

答案： 铅直 水平 $\frac{h}{l}$ 坡面 水平面

1.【概念辨析】(1)如图，修建抽水站时，沿着坡度为i = 1：6的斜坡铺设管道，下列等式成立的是( )

A. sinα = $\frac{1}{6}$
B. cosα = $\frac{1}{6}$
C. tanα = $\frac{1}{6}$
D. 以上都不对
(2)【T1(1)变式】如图，某水库堤坝横断面迎水坡AB的斜面坡度i = 1：$\sqrt{3}$，则坡角度数是______。

答案：
(1)C
(2)$30^{\circ}$

2. 如图，一山坡的坡度为i = 1：$\sqrt{3}$，小辰从山脚A出发，沿山坡向上走了200 m到达点B，则小辰上升了______m。
　

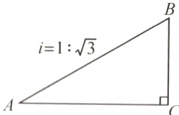
答案： 100

3.【教材P77练习T2变式】如图，某市高铁的某段路基横断面为梯形ABCD，DC//AB，BC = 6 m，试根据图中数据，求出坡角α，β的度数和斜坡AD的长.(结果保留根号)
　　　　　　　　　

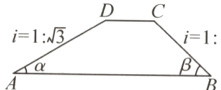
答案： 解：过点D作$DE\perp AB$于E，过点C作$CF\perp AB$于点F. 则$\angle AED=\angle BED=\angle CFA=\angle CFB = 90^{\circ}$，$\therefore DE// CF$. 又$\because CD// AB$，$\therefore$四边形DEFC是矩形. $\therefore DE = CF$. 在$Rt\triangle CBF$中，$i=\frac{CF}{BF}=1=\tan\beta$，$\therefore\beta = 45^{\circ}$. $\therefore CF = BC\cdot\sin\beta = 6\times\sin45^{\circ}=3\sqrt{2}(m)=DE$. 在$Rt\triangle AED$中，$i=\frac{DE}{AE}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$，$\therefore\alpha = 30^{\circ}$. $\therefore AD = 2DE = 2\times3\sqrt{2}=6\sqrt{2}(m)$. 答：$\alpha,\beta$分别是$30^{\circ},45^{\circ}$，$AD$长$6\sqrt{2}$m.

4. 为了学生的安全，某校决定把一段如图所示的步梯路段进行改造. 已知四边形ABCD为矩形，DE = 10 m，其坡度为i1 = 1：$\sqrt{3}$，将步梯DE改造为斜坡AF，其坡度为i2 = 1：4，求斜坡AF的长度.(结果精确到0.01 m，参考数据：$\sqrt{3}$≈1.732，$\sqrt{17}$≈4.123)
　　　　　　　　　　　　

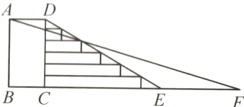
答案： 解：$\because DE = 10$m，其坡度为$i_{1}=1:\sqrt{3}$，$\therefore\angle DEC = 30^{\circ}$. 在$Rt\triangle DCE$中，$DC=\frac{1}{2}DE = 5$m. $\because$四边形ABCD为矩形，$\therefore AB = CD = 5$m. $\because$斜坡AF的坡度为$i_{2}=1:4$，$\therefore\frac{AB}{BF}=\frac{1}{4}$. $\therefore BF = 4AB = 20$m. 在$Rt\triangle ABF$中，$AF=\sqrt{AB^{2}+BF^{2}}=5\sqrt{17}\approx20.62$(m). 答：斜坡AF的长度约为20.62 m.

5.【教材P78习题T5变式】在种植树木时，负责人员要求株距(相邻两树间的水平距离)为4 m. 如图，若在坡比为1：2的山坡上种树，那么相邻两树A，C间的坡面距离AC为( )

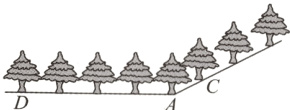
A. 2$\sqrt{5}$ m
B. 4 m
C. 8 m
D. 4$\sqrt{5}$ m　　　　　　

答案： A