《2025年名师学案九年级数学下册人教版》

7. 已知蓄电池的电压为定值，使用蓄电池时，电流I(单位：A)与电阻R(单位：Ω)是反比例函数关系，它的图象如图所示. 下列说法正确的是 ( )

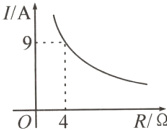
A. 函数解析式为I = $\frac{13}{R}$
B. 蓄电池的电压是18 V
C. 当I≤10 A时，R≥3.6 Ω
D. 当R = 3.6 Ω时，I = 4 A　　　　　　　　　　　　

答案： C

8.【新情境·诚信服务】要求取消市场上使用杆秤的呼声越来越高. 原因在于一些不法商贩在卖货时将秤砣挖空，或更换较小的秤砣，使秤砣较轻，从而欺骗顾客.
(1)如图，对于同一物体，哪个图用了较轻的秤砣？
　　　
(2)在称同一物体时，秤砣到支点的距离y与所用秤砣质量x之间满足______关系；
(3)当秤砣较轻时，称得的物体变重，这正好符合哪个函数的哪些性质？

答案： 解：
(1)设重物的质量为$G$，秤砣的质量为$x$，重物的受力点到支点的距离为$l$。$\because G$，$l$为定值，$xy = Gl$，且$y_{1} ＞ y_{2}$，$\therefore x_{1} ＜ x_{2}$。故图①中的秤砣较轻；
(2)反比例函数；
(3)符合反比例函数$y = \frac{Gl}{x}(x ＞ 0)$“在第一象限内，$y$随$x$的增大而减小”的性质。

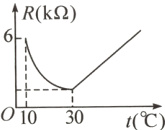
9.【一日一优】【新情境·居民生活】夏季蚊子比较活跃，家用电灭蚊器的需求量大大增加. 家用电灭蚊器的发热部分使用了PTC发热材料，它的电阻R（kΩ）随温度t（℃）（在一定范围内）变化的大致图象如图所示. 通电后，发热材料的温度在由室温10 ℃上升到30 ℃的过程中，电阻与温度成反比例关系，且在温度达到30 ℃时，电阻下降到最小值；随后电阻随温度升高而增加，温度每上升1 ℃，电阻增加$\frac{4}{15}$ kΩ.
（1）求R和t之间的函数关系式；
（2）家用电灭蚊器在使用过程中，温度在什么范围内时，发热材料的电阻不超过4 kΩ？
　　　　　　　　　　　　

答案： 解：
(1)当$10\leq t\leq30$时，设$R = \frac{k}{t}$，把$(10,6)$代入，得$k = 10×6 = 60$，$\therefore R = \frac{60}{t}$。当$t = 30$时，$R = \frac{60}{30} = 2$，$\therefore$气温为$30\ ^{\circ}C$时，电阻为$2\ k\Omega$。由题意可知，温度每上升$1\ ^{\circ}C$，电阻增加$\frac{4}{15}\ k\Omega$。$\therefore$当$t ＞ 30$时，$R = 2 + \frac{4}{15}(t - 30) = \frac{4}{15}t - 6$。$\therefore R$与$t$的函数关系式为$R = \begin{cases}\frac{60}{t}(10\leq t\leq30)\\\frac{4}{15}t - 6(t ＞ 30)\end{cases}$；
(2)当$R = 4$时，$\frac{4}{15}t - 6 = 4$，解得$t = 37.5$，$4 = \frac{60}{t}$，解得$t = 15$。$\therefore$由图象可知，当$15\ ^{\circ}C\leq t\leq37.5\ ^{\circ}C$时，发热材料的电阻不会超过$4\ k\Omega$。