《2025年名师学案九年级数学下册人教版》

由三视图求几何体的表面积或体积，应先由三视图确定几何体的________，再进一步画出________图，然后计算表面积或体积。

答案： 形状 展开

1.(2024·扬州)如图是某几何体的表面展开后得到的平面图形，则该几何体是( )

A.三棱锥
B.圆锥
C.三棱柱
D.长方体

答案： C

2.某物体的侧面展开图如图所示，那么它的左视图为( )

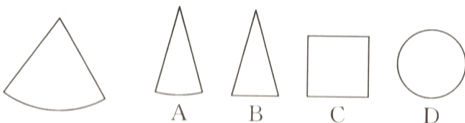
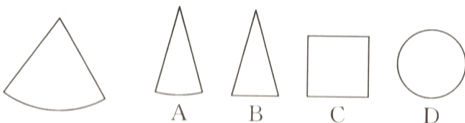
答案： B

3.(2024·包头)如图，正方形ABCD边长为2，以AB所在直线为轴，将正方形ABCD旋转一周，所得圆柱的主视图的面积为( )

A.8
B.4
C.8π
D.4π

答案： A

4.(2024·内蒙古模拟)一个几何体的三视图如图所示，则这个几何体的体积是( )

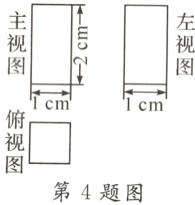
A.1 cm³
B.2 cm³
C.5 cm³
D.6 cm³

答案： B

5.(2024·东营模拟)一个几何体的三视图如图所示，则这个几何体的侧面积是( )

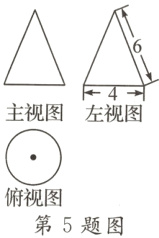
A.12π cm²
B.24π cm²
C.48π cm²
D.96π cm²

答案： A

6.【教材P101练习T2变式】一个几何体的三视图如图，则这个几何体的表面积是( )

A.39π
B.45π
C.48π
D.54π

答案： B

7.【教材P102习题T4(2)变式】如图是一个几何体的三视图.
（1）判断这个几何体的形状；
（2）根据图中数据(单位：cm)求它的表面积和体积.

答案： 解：
(1)该几何体是圆柱；
(2)圆柱表面积$=2×\pi×1^{2}+2\pi×3 = 8\pi(cm^{2})$，圆柱体积$=\pi×1^{2}×3 = 3\pi(cm^{3})$。

8.如图是一个几何体的三视图，则这个几何体的表面积是（ ）

A.18 cm²
B.20 cm²
C.(18＋2√3) cm²
D.(18＋4√3) cm²

答案： C