《2025年名师学案九年级数学下册人教版》

10. 如图所示的网格中，以点O为位似中心，四边形ABCD的位似图形是　　　(　　)

A. 四边形NPMQ
B. 四边形NPMR
C. 四边形NHMQ
D. 四边形NHMR

答案： A

11. 如图，图中的小方格都是边长为1的正方形，△ABC与△A'B'C'是以点O为位似中心的位似图形，它们的顶点都在正方形网格的格点上.
（1）画出位似中心O；
（2）△ABC与△A'B'C'的相似比是________；
（3）以点O为位似中心，在网格内再画一个△A1B1C1，使它与△ABC的相似比等于1.5.

答案：
解：
(1)位似中心O的位置如图所示；
(2)1 : 2
(3)如图所示，△A₁B₁C₁即为所求。

12.【教材P48练习T1变式】如图，△ABC与△A'B'C'是位似图形，点A，B，A'，B'，O共线，点O为位似中心.
（1）AC与A'C'平行吗？为什么？
（2）若AB = 2A'B'，OC' = 5，CC'的长是______.

答案： 解：
(1)AC//A'C'，理由如下：
∵△ABC与△A'B'C'是位似图形，
∴△ABC∽△A'B'C'。
∴∠A = ∠B'A'C'。
∴AC//A'C'。
(2)5

13.【一日一优】【新中考·新定义型阅读理解题】我们知道：如果两个三角形不仅是相似三角形，而且每对对应点所在的直线都经过同一个点，那么这两个三角形叫做位似三角形，它们的相似比又称为位似比，这个点叫做位似中心. 利用三角形的位似可以将一个三角形缩小或放大.
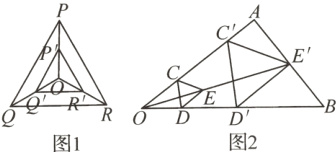
（1）如图1，点O是等边△PQR的中心，P'，Q'，R'分别是OP，OQ，OR的中点，则△P'Q'R'与△PQR是位似三角形. 此时，△P'Q'R'与△PQR的位似比是______，位似中心是______.
（2）如图2，用下面的方法可以画△AOB的内接等边三角形. 阅读后证明相应问题. 画法：
①在△AOB内画等边△CDE，使点C在OA上，点D在OB上.
②连接OE并延长，交AB于点E'，过点E'作E'C'//EC，交OA于点C'，作E'D'//ED，交OB于点D'.
③连接C'D'，则△C'D'E'是△AOB的内接三角形.
求证：△C'D'E'是等边三角形.

答案：
(1)$\frac{1}{2}$ 点O
(2)证明：
∵E'C'//EC，E'D'//ED，
∴△OCE∽△OC'E'，△ODE∽△OD'E'，
∴CE : C'E' = OE : OE'，DE : D'E' = OE : OE'，∠CEO = ∠C'E'O，∠DEO = ∠D'E'O，
∴CE : C'E' = DE : D'E'，∠CED = ∠C'E'D'，
∴△CDE∽△C'D'E'。
∵△CDE是等边三角形，
∴△C'D'E'是等边三角形。