《2025年名师学案九年级数学下册人教版》

10.【新情境·环境保护】(2024·内江)某市2021年底森林覆盖率为64%，为贯彻落实“绿水青山就是金山银山”的发展理念，该市大力发展植树造林活动，2023年底森林覆盖率已达到69%.如果这两年森林覆盖率的年平均增长率为$x$，则符合题意的方程是（ ）
A. $0.64(1 + x) = 0.69$
B. $0.64(1 + x)^{2} = 0.69$
C. $0.64(1 + 2x) = 0.69$
D. $0.64(1 + 2x)^{2} = 0.69$

答案： B

11.(中考·伊春)如图，在长为100 m，宽为50 m的矩形空地上修筑四条宽度相等的小路，若余下的部分全部种上花卉，且花圃的面积是$3600m^{2}$，则小路的宽是（ ）


A. 5 m
B. 70 m
C. 5 m或70 m
D. 10 m

答案： A

12.(2024·牡丹江)一种药品原价每盒48元，经过两次降价后每盒27元，两次降价的百分率相同，则每次降价的百分率为（ ）
A. 20%
B. 22%
C. 25%
D. 28%

答案： C

13.2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有______支队伍参加比赛.

答案： 10

14.(2024·广安)若一元二次方程$(m + 1)x^{2}-2x + 1 = 0$有两个不相等的实数根，则$m$的取值范围是（ ）
A. $m ＜ 0$且$m\neq -1$
B. $m\geq 0$
C. $m\leq 0$且$m\neq -1$
D. $m ＜ 0$

答案： A

15.(2024·绥化)小影与小冬一起写作业，在解一道一元二次方程时，小影在化简过程中写错了常数项，因而得到方程的两个根是6和1；小冬在化简过程中写错了一次项的系数，因而得到方程的两个根是 -2和 -5.则原来的方程是（ ）
A. $x^{2}+6x + 5 = 0$
B. $x^{2}-7x + 10 = 0$
C. $x^{2}-5x + 2 = 0$
D. $x^{2}-6x - 10 = 0$

答案： B

16.【新课标·传统文化】上党腊驴肉是山西长治的传统名吃，其肉质肥而不腻、瘦而不柴，香味四溢、回味无穷.某特产专卖店购进一批袋装上党腊驴肉，进价为40元/袋，经市场调查发现，当销售单价为60元时，每天可售出300袋；销售单价每降低1元，每天可多售出20袋.若销售单价降低$x$元，该专卖店每天销售这种腊驴肉可获得利润5000元，则可列方程为（ ）


A. $(60 - 40 + x)(300 + 20x) = 5000$
B. $(60 - 40 + x)(300 - 20x) = 5000$
C. $(60 - 40 - x)(300 - 20x) = 5000$
D. $(60 - 40 - x)(300 + 20x) = 5000$

答案： D

17.(2024·通辽)如图，小程的爸爸用一段10 m长的铁丝网围成一个一边靠墙(墙长5.5 m)的矩形鸭舍，其面积为$15m^{2}$，在鸭舍侧面中间位置留一个1 m宽的门(由其它材料制成)，则$BC$长为（ ）

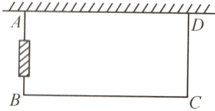
A. 5 m或6 m
B. 2.5 m或3 m
C. 5 m
D. 3 m

答案： C

18.(2024·烟台)若一元二次方程$2x^{2}-4x - 1 = 0$的两根为$m,n$，则$3m^{2}-4m + n^{2}$的值是______.

答案： 6

19.(2024·辽宁)某商场出售一种商品，经市场调查发现，日销售量$y$(件)与每件售价$x$(元)之间满足一次函数关系，部分数据如表所示：

(1)求$y$与$x$之间的函数关系式(不要求写出自变量$x$的取值范围)；
(2)该商品日销售额能否达到2600元？如果能，求出每件售价；如果不能，说明理由.

答案： 解：
(1)由题意，设一次函数的关系式为$y = kx + b$，结合表格数据知图象过$(45,55),(55,45)$，$\therefore\begin{cases}45k + b = 55\\55k + b = 45\end{cases}$，$\therefore\begin{cases}k = -1\\b = 100\end{cases}$.$\therefore y$与$x$之间的函数关系式为$y = -x + 100$；
(2)由题意，销售额为$x(-x + 100)=-x^{2}+100x$，又因为销售额为$2600$元，$\therefore2600=-x^{2}+100x$.$\therefore x^{2}-100x + 2600 = 0$.$\therefore\Delta=(-100)^{2}-4\times2600 = 10000 - 10400=-400＜0$.$\therefore$方程没有实数根，故该商品日销售额不能达到$2600$元.