《2025年名师学案九年级数学下册人教版》

1. 若圆柱的体积是V，则它的底面积S与其高度h的关系式是________.

答案： $S = \frac{V}{h}$

2. 工作总量W一定，则工作效率v与工作时间t的关系式是________.

答案： $v = \frac{W}{t}$

1.【新情境·居民生活】为打赢“蓝天保卫战”，某市为保障清洁取暖，实行“煤改气”.如图，该市煤气公司计划在地下修建一个容积为10⁴m³的圆柱形煤气储存室，则储存室的底面积S(m²)与其深度d(m)的函数图象大致是 （ ）

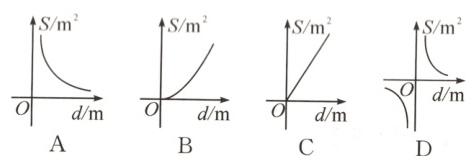
答案： A

2. 某学校要种植一块面积为100 m²的长方形草坪，要求两边长均不小于5 m，则草坪的一边长y(单位：m)随另一边长x(单位：m)的变化而变化的图象可能是 （ ）

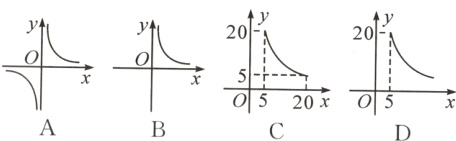
【点拨】根据长方形的面积公式得xy = 100，变形求出y与x之间的函数关系式，再结合已知条件x≥5，y≥5，求出x的取值范围确定答案.

答案： C

3. 验光师测得的一组关于近视眼镜的度数y与镜片的焦距x的数据如下表：

则y关于x的函数解析式是________.

答案： $y = \frac{100}{x}$

4.【教材P13例2变式】码头工人往一艘轮船上装载货物，装完货物所需的时间y(min)与装载速度x(t/min)之间的函数关系如图(双曲线y = $\frac{k}{x}$的一支).如果以5 t/min的速度卸货，那么卸完货物需要______min.

答案： 120

5. 某厂仓库储存了部分原料，按原计划每小时消耗2吨，可用60小时. 由于技术革新，实际生产能力有所提高，即每小时消耗的原料量大于计划消耗的原料量. 设现在每小时消耗原料x(单位：吨)，库存的原料可使用的时间为y(单位：小时).
(1)y关于x的函数解析式是__________，自变量x的取值范围是________；
(2)若恰好经过24小时才有新的原料进厂，为了使机器不停止运转，则x应控制在什么范围内?

答案：
(1) $y = \frac{120}{x}$ $x＞2$ 解：
(2)由
(1)知 $y = \frac{120}{x}$，当 $y = 24$ 时，$x = 5$，对于函数 $y = \frac{120}{x}$，当 $x＞0$ 时，$x$ 越大，$y$ 越小，
∴当 $x$ 取最大值 5 时，$y$ 有最小值 24.
∴$x$ 应控制的范围为 $2＜x\leqslant5$.