第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 在Rt△ABC中,当锐角A的度数一定时,∠A的对边与斜边的比都是一个________.
答案:
固定值
2. 在Rt△ABC中,∠C = 90°,锐角A的对边与________的比叫做∠A的正弦,记作________,即sinA = ________ = ________.
答案:
斜边 sinA $\frac{\angle A的对边}{斜边}$ $\frac{a}{c}$
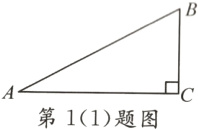
1. (1)(2024·云南改编)如图,在△ABC中,∠C = 90°,AB = 13,BC = 5,则sinA等于 ( )
A. $\frac{13}{5}$ B. $\frac{5}{12}$ C. $\frac{5}{13}$ D. $\frac{12}{13}$
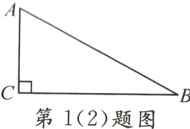
(2)【T1(1)变式】如图,在Rt△ABC中,∠C = 90°,AC = 5,BC = 12,则sinB的值是 ( )
A. $\frac{5}{13}$ B. $\frac{12}{13}$ C. $\frac{12}{5}$ D. $\frac{5}{12}$
A. $\frac{13}{5}$ B. $\frac{5}{12}$ C. $\frac{5}{13}$ D. $\frac{12}{13}$

(2)【T1(1)变式】如图,在Rt△ABC中,∠C = 90°,AC = 5,BC = 12,则sinB的值是 ( )
A. $\frac{5}{13}$ B. $\frac{12}{13}$ C. $\frac{12}{5}$ D. $\frac{5}{12}$

答案:
(1)C
(2)A
(1)C
(2)A
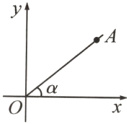
2. 如图,在平面直角坐标系中,点A(12,9),那么sinα的值是 ( )
A. $\frac{5}{3}$ B. $\frac{5}{4}$
C. $\frac{3}{5}$ D. $\frac{4}{5}$
A. $\frac{5}{3}$ B. $\frac{5}{4}$
C. $\frac{3}{5}$ D. $\frac{4}{5}$

答案:
C
3. 在Rt△ABC中,∠C = 90°,a,b,c分别是∠A,∠B,∠C的对边.若2b = $\sqrt{2}$c,则∠B的正弦值等于________.
答案:
$\frac{\sqrt{2}}{2}$
4.【教材P63例1变式】如图,在△ABC中,∠C = 90°,AC : BC = 3 : 2,求sinA和sinB的值.
解:设AC = 3a,则BC = 2a,在Rt△ABC中,AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{(3a)^{2}+(2a)^{2}}$ = ________,
∴sinA = $\frac{BC}{( )}$ = $\frac{2a}{( )}$ = ________,
sinB = $\frac{AC}{( )}$ = $\frac{3a}{( )}$ = ________.
解:设AC = 3a,则BC = 2a,在Rt△ABC中,AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{(3a)^{2}+(2a)^{2}}$ = ________,
∴sinA = $\frac{BC}{( )}$ = $\frac{2a}{( )}$ = ________,
sinB = $\frac{AC}{( )}$ = $\frac{3a}{( )}$ = ________.

答案:
$\sqrt{13}a$ AB $\sqrt{13}a$ $\frac{2}{13}\sqrt{13}$ AB $\sqrt{13}a$ $\frac{3}{13}\sqrt{13}$
5. 直角三角形的两边长为3和4,则较小锐角的正弦值是________.
【点拨】当直角三角形的边不确定时,应分类讨论,即①3和4是直角边长;②4是斜边长,3是直角边长,再根据正弦的定义解答.
【点拨】当直角三角形的边不确定时,应分类讨论,即①3和4是直角边长;②4是斜边长,3是直角边长,再根据正弦的定义解答.
答案:
$\frac{3}{5}$或$\frac{\sqrt{7}}{4}$
6. 在Rt△ABC中,∠B = 90°,sinA = $\frac{3}{5}$,AC = 100,则BC等于 ( )
A. $\frac{500}{3}$
B. $\frac{503}{5}$
C. 60
D. 80
A. $\frac{500}{3}$
B. $\frac{503}{5}$
C. 60
D. 80
答案:
C
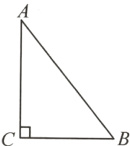
7. 如图,在△ABC中,∠C = 90°,sinA = $\frac{12}{13}$,BC = 12,求AC和AB的长.

答案:
解:在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\sin A=\frac{BC}{AB}=\frac{12}{AB}=\frac{12}{13}$,解得$AB = 13$. $\therefore AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{13^{2}-12^{2}} = 5$.
查看更多完整答案,请扫码查看


