《2025年名师学案九年级数学下册人教版》

在日常生活中，我们可以借助光线或视线来构造相似三角形，然后利用相似三角形的对应边________来计算不能直接测量的河的宽度或物体的高度.

答案： 成比例

1.【新情境·视力保护】为了加强视力保护意识，小明要在书房里挂一张视力表.由于书房空间狭小，他想根据测试距离为5 m的大视力表制作一个测试距离为3 m的小视力表.如图，如果大视力表中的“E”的高度是3.5 cm，那么小视力表中相应“E”的高度是 （ ）

A.3 cm
B.2.5 cm
C.2.3 cm
D.2.1 cm

答案： D

2.【新课标·跨物理学科】如图是小明设计用手电测量某古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2 m，BP=1.8 m，PD=12 m，那么该古城墙的高度是 （ ）

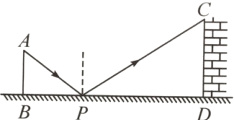
A.6 m
B.8 m
C.18 m
D.24 m

答案： B

3.【教材P40例6变式】九年级（1）班课外活动小组利用标杆测量学校旗杆的高度.已知标杆高度CD=3 m，标杆与旗杆的水平距离BD=15 m，人的眼睛与地面的高度EF=1.6 m，人与标杆CD的水平距离DF=2 m，求旗杆AB的高度.

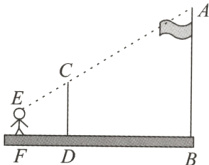
答案： 解：过点E作EH⊥AB于点H，交CD于点G. 由题意，得CG//AH，
∴△CGE∽△AHE.
∴$\frac{CG}{AH}=\frac{EG}{EH}$.
∵$\frac{3 - 1.6}{AH}=\frac{2}{15 + 2}$，解得AH = 11.9.
∴AB = AH + HB
= AH + EF = 11.9 + 1.6 = 13.5(m). 答：旗杆AB的高度是13.5 m.

4.【新情境·居民生活】如图是某晾衣架的侧面示意图，根据图中数据，则C，D两点间的距离是 （ ）

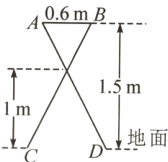
A.0.9 m
B.1.2 m
C.1.5 m
D.2.5 m

答案： B

5.【新课标·数学文化】《九章算术》中记载了一种测量井深的方法.如图，在井口B处立一根垂直于井口的木杆BD，从木杆的顶端D观察井水水岸C，视线DC与井口的直径AB交于点E.如果测得AB=1.6 m，BD=1 m，BE=0.2 m，那么AC的长为______m.

答案： 7

6.【教材P40例5变式】如图，为测量出湖边不可直接到达的A，B两点间的距离，测量人员选取一定点O，使点A，O，C和点B，O，D分别在同一条直线上，测出CD=150 m，且OB=3OD，OA=3OC，则AB=______m.

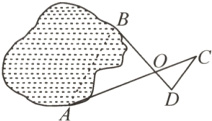
答案： 450