第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
8. 如图,点A为∠α边上任意一点,作AC⊥BC 于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是 ( )
A. $\frac{CD}{AC}$ B. $\frac{BC}{AB}$ C. $\frac{BD}{BC}$ D. $\frac{AD}{AC}$

A. $\frac{CD}{AC}$ B. $\frac{BC}{AB}$ C. $\frac{BD}{BC}$ D. $\frac{AD}{AC}$

答案:
D
9. 如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tanB为 ( )
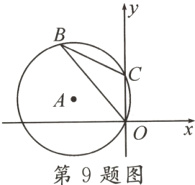
A. 2
B. 2$\sqrt{2}$
C. $\frac{\sqrt{2}}{4}$
D. $\frac{2\sqrt{2}}{3}$

A. 2
B. 2$\sqrt{2}$
C. $\frac{\sqrt{2}}{4}$
D. $\frac{2\sqrt{2}}{3}$
答案:
C
10. [教材P85复习题T11变式]如图,在矩形ABCD中,AB = 8,BC = 10,点E是AB边上一点,将四边形CDAE沿CE折叠,点A,D的对应点分别为A',D',若A'D'恰好经过点B,则∠A'EB 的余弦值为________.


答案:
$\frac{3}{5}$
11. [新课标.操作能力]如图是由边长相等的小正方形组成的网格,点A,B,C均在格点上,连接AB,BC.
(1) tan∠ABC = ________;
(2) 在网格中,用无刻度的直尺画∠CBD,使tan∠CBD = $\frac{2}{3}$.
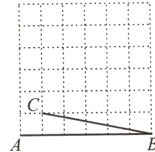
(1) tan∠ABC = ________;
(2) 在网格中,用无刻度的直尺画∠CBD,使tan∠CBD = $\frac{2}{3}$.

答案:
(1)$\frac{1}{5}$ 解:
(2)如图,$\angle CBD$即为所求.
(1)$\frac{1}{5}$ 解:
(2)如图,$\angle CBD$即为所求.

12. 如图,在平面直角坐标系内,O为原点,点A 的坐标为(10,0),点B在第一象限内,BO = 5,sin∠BOA = $\frac{3}{5}$.
(1) 点B的坐标是________;
(2) 求cos∠BAO的值.
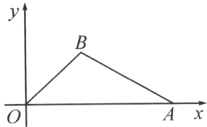
(1) 点B的坐标是________;
(2) 求cos∠BAO的值.

答案:
(4,3) 解:
(2)过B作$BC\perp OA$于C.$\because B(4,3)$,$BC\perp OA$,$\therefore OC = 4$,$BC = 3$.$\because A(10,0)$,$\therefore AC = 10 - 4 = 6$.$\therefore AB=\sqrt{6^{2}+3^{2}} = 3\sqrt{5}$.$\therefore\cos\angle BAO=\frac{AC}{AB}=\frac{6}{3\sqrt{5}}=\frac{2}{5}\sqrt{5}$.
(2)过B作$BC\perp OA$于C.$\because B(4,3)$,$BC\perp OA$,$\therefore OC = 4$,$BC = 3$.$\because A(10,0)$,$\therefore AC = 10 - 4 = 6$.$\therefore AB=\sqrt{6^{2}+3^{2}} = 3\sqrt{5}$.$\therefore\cos\angle BAO=\frac{AC}{AB}=\frac{6}{3\sqrt{5}}=\frac{2}{5}\sqrt{5}$.
13. [一日一优][新中考.新定义型阅读理解题]定义:如图,在Rt△ABC中,锐角α的邻边与对边的比叫做∠α的余切,记作cotα,即cotα = $\frac{∠α的邻边}{∠α的对边}$ = $\frac{AC}{BC}$.据上述角的余切定义,解答下列问题:
(1) cot30° = ______;
(2) 如图,在Rt△ABC中,tanA = $\frac{3}{4}$,试求cotA的值.
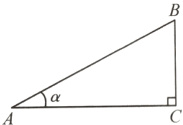
(1) cot30° = ______;
(2) 如图,在Rt△ABC中,tanA = $\frac{3}{4}$,试求cotA的值.

答案:
$\sqrt{3}$
解:在$Rt\triangle ABC$中,$\tan A=\frac{BC}{AC}=\frac{3}{4}$,$\therefore\frac{AC}{BC}=\frac{4}{3}$.$\therefore\cot A=\frac{4}{3}$.
解:在$Rt\triangle ABC$中,$\tan A=\frac{BC}{AC}=\frac{3}{4}$,$\therefore\frac{AC}{BC}=\frac{4}{3}$.$\therefore\cot A=\frac{4}{3}$.
查看更多完整答案,请扫码查看


