《2025年名师学案九年级数学下册人教版》

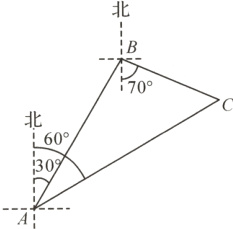
6. 如图，一艘货轮在海面上航行，准备要停靠到码头C，货轮航行到A处时，测得码头C在北偏东60°的方向上. 为了躲避A，C之间的暗礁，这艘货轮调整航向，沿着北偏东30°的方向继续航行，当它航行到B处后，又沿着南偏东70°的方向航行40海里到达码头C.（参考数据：sin 50°≈0.766，cos 50°≈0.643，tan 50°≈1.192）
（1）则∠ACB的度数是______；
（2）求货轮从A处到B处航行的距离（结果精确到0.1海里）.

答案：
(1)$50^{\circ}$
(2)解：过点B作$BE\perp AC$于E，在$Rt\triangle BEC$中，$BC = 40$海里，$\angle C = 50^{\circ}$，$\because\sin C=\frac{BE}{BC}$，$\therefore BE = BC\cdot\sin C\approx40\times0.766 = 30.64$（海里）. 在$Rt\triangle ABE$中，$\angle BAE = 30^{\circ}$，则$AB = 2BE = 2\times30.64\approx61.3$（海里）. 答：货轮从A到B航行的距离约为61.3海里.

7.【一日一优】（2024·重庆）如图，甲、乙两艘货轮同时从A港出发，分别向B，D两港运送物资，最后到达A港正东方向的C港装运新的物资. 甲货轮沿A港的东南方向航行40海里后到达B港，再沿北偏东60°方向航行一定距离到达C港. 乙货轮沿A港的北偏东60°方向航行一定距离到达D港，再沿南偏东30°方向航行一定距离到达C港.（参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，$\sqrt{6}$≈2.45）
（1）求A，C两港之间的距离（结果保留小数点后一位）；
（2）若甲、乙两艘货轮的速度相同（停靠B，D两港的时间相同），哪艘货轮先到达C港？请通过计算说明.

答案： 解：
(1)过点B作$BE\perp AC$，垂足为E，在$Rt\triangle ABE$中，$\angle BAE = 45^{\circ}$，$AB = 40$海里，$\therefore AE = AB\cdot\cos45^{\circ}=20\sqrt{2}$（海里）$= BE$. 在$Rt\triangle BCE$中，$\angle CBE = 60^{\circ}$，$\therefore CE = BE\cdot\tan60^{\circ}=20\sqrt{2}\times\sqrt{3}=20\sqrt{6}$（海里）. $\therefore AC = AE + CE = 20\sqrt{2}+20\sqrt{6}\approx77.2$（海里）. 答：A，C两港之间的距离约为77.2海里；
(2)甲货轮先到达C港，理由：由题意，得$\angle CDF = 30^{\circ}$，$DF// AG$，$\therefore\angle GAD=\angle ADF = 60^{\circ}$. $\therefore\angle ADC=\angle ADF+\angle CDF = 90^{\circ}$. 在$Rt\triangle ACD$中，$\angle CAD = 90^{\circ}-\angle GAD = 30^{\circ}$，$\therefore CD=\frac{1}{2}AC=(10\sqrt{2}+10\sqrt{6})$海里，$AD=\sqrt{3}CD=(10\sqrt{6}+30\sqrt{2})$海里. 在$Rt\triangle BCE$中，$\angle CBE = 60^{\circ}$，$BE = 20\sqrt{2}$海里，$\therefore BC=\frac{BE}{\cos60^{\circ}}=40\sqrt{2}$（海里）. $\therefore$甲货轮航行的路程$=AB + BC = 40 + 40\sqrt{2}\approx96.4$（海里），乙货轮航行的路程$=AD + CD = 10\sqrt{6}+30\sqrt{2}+10\sqrt{2}+10\sqrt{6}=20\sqrt{6}+40\sqrt{2}\approx105.4$（海里）. $\because96.4$海里$＜105.4$海里，$\therefore$甲货轮先到达C港.