第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
9. 已知三条线段的长分别为1 cm,2 cm,$\sqrt{2}$ cm,如果另外一条线段与它们是成比例线段,那么另外一条线段的长是______.
【点拨】成比例线段具有顺序性,应分类讨论后计算.
【点拨】成比例线段具有顺序性,应分类讨论后计算.
答案:
9.$\sqrt{2}$cm或2$\sqrt{2}$cm或$\frac{\sqrt{2}}{2}$cm
10. 如图,有三个矩形,其中相似的是 ( )
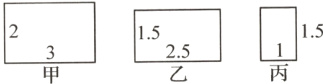
A. 甲和乙
B. 甲和丙
C. 乙和丙
D. 甲、乙和丙
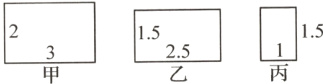
A. 甲和乙
B. 甲和丙
C. 乙和丙
D. 甲、乙和丙
答案:
10.B
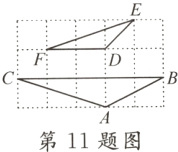
11. 如图,在3×5网格中,△ABC和△DEF相似,则∠BAC的度数是______.

答案:
11.135°
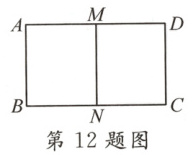
12.【教材P28习题T8变式】如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB = 4,则AD的长是______.

答案:
12.4$\sqrt{2}$
13.【教材P27习题T4变式】下面左图有一个图形,请在右图中画出所给图形的相似图形,使新图形的各顶点仍在格点上.
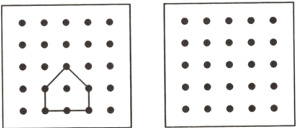

答案:
13.解:如图所示.
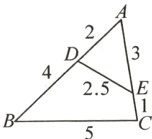
14.【教材P28习题T5变式】如图,点D,E分别在△ABC的边AB和AC上,AD = 2,BD = 4,AE = 3,CE = 1,DE = 2.5,BC = 5,∠ADE = ∠C.
(1)求$\frac{AD}{AC}$,$\frac{AE}{AB}$,$\frac{DE}{BC}$的值;
(2)求证:△ADE与△ACB相似.
(1)求$\frac{AD}{AC}$,$\frac{AE}{AB}$,$\frac{DE}{BC}$的值;
(2)求证:△ADE与△ACB相似.

答案:
14.
(1)解:
∵AD = 2,BD = 4,AE = 3,CE = 1,DE = 2.5,BC = 5,
∴AB = 2 + 4 = 6,AC = 3 + 1 = 4,
∴$\frac{AD}{AC}=\frac{2}{4}=\frac{1}{2}$,$\frac{AE}{AB}=\frac{3}{6}=\frac{1}{2}$,$\frac{DE}{CB}=\frac{2.5}{5}=\frac{1}{2}$;
(2)证明:由
(1)知$\frac{AD}{AC}=\frac{AE}{AB}=\frac{DE}{CB}=\frac{1}{2}$.在△ADE和△ACB中,∠A = ∠A,∠ADE = ∠C,
∴∠AED = ∠B,
∴△ADE和△ACB相似.
(1)解:
∵AD = 2,BD = 4,AE = 3,CE = 1,DE = 2.5,BC = 5,
∴AB = 2 + 4 = 6,AC = 3 + 1 = 4,
∴$\frac{AD}{AC}=\frac{2}{4}=\frac{1}{2}$,$\frac{AE}{AB}=\frac{3}{6}=\frac{1}{2}$,$\frac{DE}{CB}=\frac{2.5}{5}=\frac{1}{2}$;
(2)证明:由
(1)知$\frac{AD}{AC}=\frac{AE}{AB}=\frac{DE}{CB}=\frac{1}{2}$.在△ADE和△ACB中,∠A = ∠A,∠ADE = ∠C,
∴∠AED = ∠B,
∴△ADE和△ACB相似.
15.【一日一优】【新中考·新定义型阅读理解题】宽与长的比是$\frac{\sqrt{5}-1}{2}$(约为0.618)的矩形叫做黄金矩形. 黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感. 我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF;以点F为圆心,以FD的长为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H. 则下列矩形是黄金矩形的是 ( )
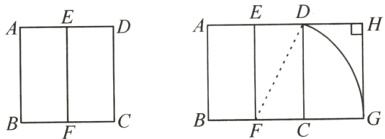
A. 矩形ABFE
B. 矩形EFCD
C. 矩形EFGH
D. 矩形DCGH

A. 矩形ABFE
B. 矩形EFCD
C. 矩形EFGH
D. 矩形DCGH
答案:
15.D
查看更多完整答案,请扫码查看


