《2025年名师学案九年级数学下册人教版》

活动1:在数学活动课上，“腾飞”小组的同学们参加了人教九年级下册第19页“活动2”的探究活动.如图1，在左侧托盘A(固定)中放置一个重物，在右侧托盘B(可左右移动)中放置一定质量的砝码，可使得仪器左右平衡.改变托盘B与点O的距离，保持仪器平衡，记录相应的托盘B中的砝码质量，得到如下相关数据：

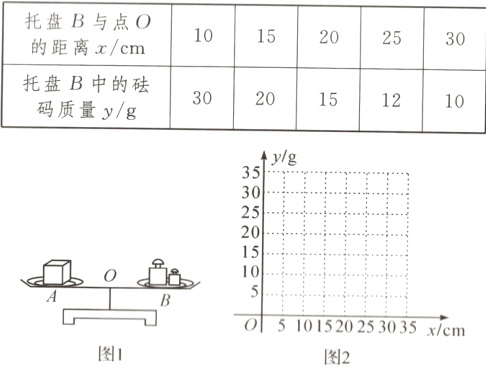
(1)根据表格中的数值在图2的平面直角坐标系中描出相应的点、并用平滑的曲线连接这些点;
(2)观察所画的图象，写出y与x的函数关系式并加以验证;
(3)当砝码质量为24g时，托盘B与点O的距离是____________;
(4)当托盘B向左移动(不能移动到点O)时，应往托盘B中添加砝码还是减少砝码？为什么？

答案： 解:
(1)描点、连线略;
(2)设y与x之间的函数关系式是$y = \frac{k}{x}$,把(10,30)代入,解得$k = 300$.所以$y=\frac{300}{x}$.将其余各点分别代入$y=\frac{300}{x}$验证均适合,$\therefore y$与$x$的函数关系式为$y=\frac{300}{x}$;
(3)12.5cm　
(4)根据反比例函数的增减性,当$x$变小时,$y$变大,故当托盘$B$与点$O$的距离不断减小时，即$x$变小,此时$y$变大,$\therefore$应往托盘$B$中添加砝码.

活动2:如图所示的一架自制天平，支点O固定不变，左侧托盘固定在点A处，右侧托盘的点P可以在横梁BC段滑动.已知OA=OC=12cm，BC=28cm，一个100g的砝码.

由于一个空的矿泉水瓶太轻无法称量，请各小组利用活动1的结论探究如何称量一个空矿泉水瓶的质量？写出活动方案并求空矿泉水瓶的质量.

答案：
解:左侧托盘放置砝码，右侧托盘放置矿泉水瓶，如下图:
　　　　　　 　　　　　
方案:(答案不唯一)滑动点$P$至点$B$,空瓶中加入适量的水使天平平衡，再向瓶中加入等量的水，发现点$P$移动到$PC$长为12cm时，天平平衡.设第一次加入水的质量为$a$(g),空矿泉水瓶的质量为$b$(g).第一次称量时,$x = OB = 40$,$y = a + b$,根据杠杆原理列出方程:$40(a + b)=1200$.第二次称量时,$x = OC + PC = 12 + 12 = 24$,$y = 2a + b$,根据杠杆原理列出方程:$24(2a + b)=1200$.可得方程组$\begin{cases}40(a + b)=1200\\24(2a + b)=1200\end{cases}$,解得$\begin{cases}a = 20\\b = 10\end{cases}$.答:空矿泉水瓶的质量为10g.