《2025年名师学案九年级数学下册人教版》

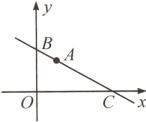
1. 如图，直线l经过点A(2,3)和点B(0,4)，与x轴交于点C.
(1)直线l的解析式为____________；
(2)在y轴上是否存在一点P，使得以A，B，P为顶点的三角形与△OBC相似？若存在，请求出点P的坐标；若不存在，请说明理由.
　　　　

答案：
(1)$y = -\frac{1}{2}x + 4$ 解：
(2)存在点$P$，使得以$A$，$B$，$P$为顶点的三角形与$\triangle OBC$相似，理由如下：当$y = 0$时，$x = 8$，$\therefore C(8,0)$.$\therefore OB = 4$，$OC = 8$.$\therefore \frac{OB}{OC}=\frac{1}{2}$.$\because \triangle OBC$是直角三角形，$\therefore \triangle APB$也是直角三角形. 当$\angle APB = 90^{\circ}$时，$P(0,3)$. 此时$BP = 1$，$PA = 2$，$\therefore \frac{PB}{AP}=\frac{1}{2}$. 此时$\triangle OBC\sim\triangle PBA$；当$\angle PAB = 90^{\circ}$时，$\angle OCB = \angle APB$.$\therefore \frac{AB}{AP}=\frac{1}{2}$，即$AP = 2AQ = 2\sqrt{5}$，$\therefore BP=\sqrt{AB^{2}+AP^{2}} = 5$，$\therefore P(0,-1)$；综上所述，$P$点坐标为$(0,3)$或$(0,-1)$

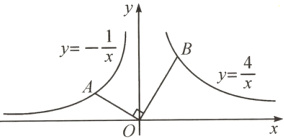
2. (2024·苏州)如图，点A为反比例函数y = - $\frac{1}{x}$(x＜0)图象上的一点，连接AO，过点O作OA的垂线与反比例函数y = $\frac{4}{x}$的图象交于点B. 则$\frac{AO}{BO}$的值为（ ）
　　
A. $\frac{1}{2}$
B. $\frac{1}{4}$
C. $\frac{\sqrt{3}}{3}$
D. $\frac{1}{3}$

答案： A

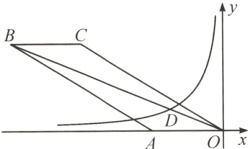
3. (2024·绥化)如图，点A(-7,0)，B(x,10)，C(-17,y)，在平行四边形ABCO中，它的对角线OB与反比例函数y = $\frac{k}{x}$(k≠0)的图象相交于点D，且OD∶OB = 1∶4，则k的值是________.
　　

答案： -15

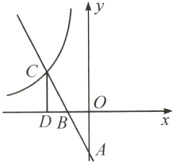
4. (2024·南充)如图，直线y = kx + b经过A(0,-2)，B(-1,0)两点，与双曲线y = $\frac{m}{x}$(x＜0)交于点C(a,2).
(1)直线的解析式是____________，双曲线的解析式是____________；
(2)过点C作CD⊥x轴于点D，点P在x轴上，若以O，A，P为顶点的三角形与△BCD相似，求点P的坐标.
　　　　　　　

答案：
(1)$y = -2x - 2$ $y = -\frac{4}{x}$ 解：
(2)$\because CD\perp x$轴，$C(-2,2)$，$\therefore D(-2,0)$，$CD = 2$.$\because B(-1,0)$，$\therefore BD = 1$.$\because A(0,-2)$，$\therefore OA = 2$. 若以$O$，$A$，$P$为顶点的三角形与$\triangle BCD$相似，则分两种情况：①当$\triangle AOP\sim\triangle BDC$时，$\frac{AO}{BD}=\frac{OP}{DC}$，即$\frac{2}{1}=\frac{OP}{2}$.$\therefore OP = 4$. ②当$\triangle AOP\sim\triangle CDB$时，$\frac{AO}{CD}=\frac{OP}{BD}$，即$\frac{2}{2}=\frac{OP}{1}$.$\therefore OP = 1$.$\because$点$P$在$x$轴上，$\therefore$点$P$坐标为$(-4,0)$或$(-1,0)$或$(1,0)$或$(4,0)$.