第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.【新课标·过程性学习】探究函数图象与性质时,勇毅班同学根据学习函数的经验,对函数$y=\frac{x}{x - 1}$的图象与性质进行了探究,下面是勤奋小组同学记录的探究过程,请你补充完整.
(1)函数$y=\frac{x}{x - 1}$的自变量$x$的取值范围是________;
(2)列出$y$与$x$的对应值,请直接写出$a$,$b$的值:$a =$________,$b =$________;
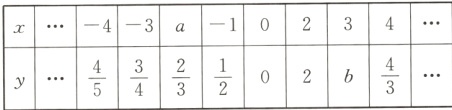
(3)在平面直角坐标系$xOy$中,描出表格中各对对应值,并画出图象;

(4)请写出函数$y=\frac{x}{x - 1}$的一条性质.
(1)函数$y=\frac{x}{x - 1}$的自变量$x$的取值范围是________;
(2)列出$y$与$x$的对应值,请直接写出$a$,$b$的值:$a =$________,$b =$________;

(3)在平面直角坐标系$xOy$中,描出表格中各对对应值,并画出图象;

(4)请写出函数$y=\frac{x}{x - 1}$的一条性质.
答案:
(1)$x\neq1$
(2)$-2$ $1.5$
解:
(3)画图如图所示
 ;
;
(4)由图象可知,当$x < 1$时,$y$随$x$的增大而减小(答案不唯一).
(1)$x\neq1$
(2)$-2$ $1.5$
解:
(3)画图如图所示
 ;
;(4)由图象可知,当$x < 1$时,$y$随$x$的增大而减小(答案不唯一).
2.(2024·宁夏)在同一平面直角坐标系中,函数$y = 2x + 1$的图象可以由函数$y = 2x$的图象平移得到.依此想法,数学小组对反比例函数图象的平移进行探究.
【动手操作】
列表:

描点连线:在已画出函数$y=\frac{2}{x}$的图象的坐标系中画出函数$y=\frac{2}{x + 1}$的图象.

【探究发现】
(1)将反比例函数$y=\frac{2}{x}$的图象向左平移______个单位长度得到函数$y=\frac{2}{x + 1}$的图象.
(2)上述探究方法运用的数学思想是______.
A.整体思想
B.类比思想
C.分类讨论思想
【应用延伸】
(1)将反比例函数$y = -\frac{1}{x}$的图象先________得到函数$y = -\frac{1}{x - 2}-1$的图象;
(2)函数$y = -\frac{1}{x - 2}-1$图象的对称中心的坐标为__________.
【动手操作】
列表:

描点连线:在已画出函数$y=\frac{2}{x}$的图象的坐标系中画出函数$y=\frac{2}{x + 1}$的图象.

【探究发现】
(1)将反比例函数$y=\frac{2}{x}$的图象向左平移______个单位长度得到函数$y=\frac{2}{x + 1}$的图象.
(2)上述探究方法运用的数学思想是______.
A.整体思想
B.类比思想
C.分类讨论思想
【应用延伸】
(1)将反比例函数$y = -\frac{1}{x}$的图象先________得到函数$y = -\frac{1}{x - 2}-1$的图象;
(2)函数$y = -\frac{1}{x - 2}-1$图象的对称中心的坐标为__________.
答案:
解:画图略 [探究发现]
(1)$1$
(2)B [应用延伸]
(1)向右平移$2$个单位长度,再向下平移$1$个单位长度
(2)$(2,-1)$
(1)$1$
(2)B [应用延伸]
(1)向右平移$2$个单位长度,再向下平移$1$个单位长度
(2)$(2,-1)$
查看更多完整答案,请扫码查看


