《2025年名师学案九年级数学下册人教版》

7. 如图，点P₁，P₂，P₃，P₄均在坐标轴上，且P₁P₂⊥P₂P₃，P₂P₃⊥P₃P₄. 若点P₁，P₂的坐标分别为(0，-1)，(-2，0)，则点P₄的坐标为______.

答案： $(8,0)$

8. 如图，在△ABC和△ADE中，∠BAD = ∠CAE，∠ABD = ∠ACE. 求证：
(1)$\frac{AB}{AC}=\frac{AD}{AE}$；
(2)△ADE∽△ABC.

答案： 证明:
(1)
∵$\angle BAD=\angle CAE$，$\angle ABD=\angle ACE$，
∴$\triangle ABD\sim\triangle ACE$，$\frac{AB}{AC}=\frac{AD}{AE}$；
(2)
∵$\triangle ABD\sim\triangle ACE$，
∴$\frac{AB}{AC}=\frac{AD}{AE}$。又
∵$\angle BAD=\angle CAE$，
∴$\angle BAD + \angle DAC=\angle DAC+\angle CAE$，即$\angle BAC=\angle DAE$。
∵$\frac{AB}{AC}=\frac{AD}{AE}$，
∴$\frac{AB}{AD}=\frac{AC}{AE}$，
∴$\triangle ADE\sim\triangle ABC$。

9. 点P在四边形ABCD的对角线AC上，直角三角板PEF的直角边PE，PF分别交AB，BC边于点M，N.
【特例探究】
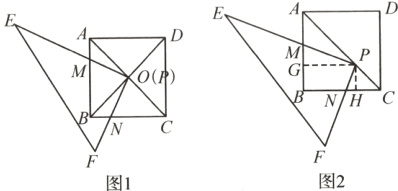
(1)如图1，若O是边长为2的正方形ABCD对角线AC，BD的交点，当点P在点O处时，无论三角板PEF绕点O怎样转动，我们发现，三角板与正方形重叠部分的面积总等于______；
【类比探究】
(2)如图2，在(1)的条件下，改变点P的位置(P在对角线AC上)，若PA∶PC = k，则有PM = kPN. 下面是该结论的证明过程：
证明：过点P作PG⊥AB于点G，作PH⊥BC于点H，
……
请按以上证明思路完成剩余的证明过程.

答案：
(1) 1
(2) 证明:
∵四边形$ABCD$是正方形，
∴$\angle B = 90^{\circ}$，$\angle BAC=\angle BCA = 45^{\circ}$。
∵$PG\perp AB$，$PH\perp BC$，
∴$\triangle AGP$，$\triangle CHP$是等腰直角三角形，$\angle PGB=\angle PHB = 90^{\circ}$，$\angle PGM=\angle PHN$。
∴$PG=\frac{\sqrt{2}}{2}PA$，$PH=\frac{\sqrt{2}}{2}PC$，$\angle GPH = 90^{\circ}$，
∴$\frac{PG}{PH}=\frac{PA}{PC}=k$。
∵$\angle EPF=\angle GPH = 90^{\circ}$，
∴$\angle MPG=\angle NPH$。
∵$\angle PGM=\angle PHN = 90^{\circ}$，
∴$\triangle PGM\sim\triangle PHN$，
∴$\frac{PM}{PN}=\frac{PG}{PH}=k$，
∴$PM = kPN$。