《2025年名师学案九年级数学下册人教版》

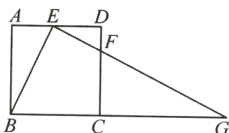
10. 如图，在正方形ABCD中，E为边AD的中点，点F在边CD上，∠BEF = 90°.
(1)求证：△ABE∽△DEF；
(2)若AB = 4，延长EF交BC的延长线于点G，求CG的长.

答案：
(1) 证明:
∵四边形$ABCD$为正方形，
∴$\angle A=\angle D = 90^{\circ}$，
∴$\angle ABE+\angle AEB = 90^{\circ}$。
∵$\angle BEF = 90^{\circ}$，
∴$\angle AEB+\angle DEF = 90^{\circ}$，
∴$\angle ABE=\angle DEF$，
∴$\triangle ABE\sim\triangle DEF$；
(2) 解:
∵四边形$ABCD$是正方形，
∴$AB = AD = BC = 4$。
∵$E$为$AD$的中点，
∴$AE = DE=\frac{1}{2}AD = 2$。由
(1)知，$\triangle ABE\sim\triangle DEF$，
∴$\frac{AB}{DE}=\frac{AE}{DF}$，即$\frac{4}{2}$$=\frac{2}{DF}$，
∴$DF = 1$，
∴$CF = CD - DF = 4 - 1 = 3$。
∵$ED// CG$，
∴$\triangle EDF\sim\triangle GCF$，
∴$\frac{ED}{GC}=\frac{DF}{CF}$，即$\frac{2}{GC}=\frac{1}{3}$，
∴$GC = 6$。

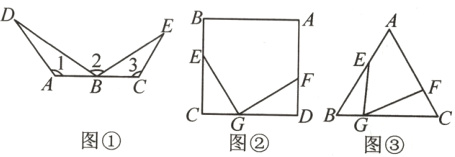
11.【问题引入】如图①，点A，B，C在同一条直线上，∠1 = ∠2 = ∠3，求证：AB·BC = AD·CE；
【探索应用】如图②，在边长为6的正方形ABCD中，G，E分别是CD，CB上的动点，连接EG，作GF⊥EG交AD于F. 若GC = 2，求证：CE·DF是定值；
【拓展延伸】如图③，等边△ABC中，BC = 6，G是BC上一点(不与B，C重合)，E在AB上，F在AC上，且∠EGF = 60°，则BE·CF的最大值是______.

答案： 【问题引入】证明:
∵$\angle DBC=\angle 2+\angle EBC=\angle 1+\angle D$，$\angle 1=\angle 2$，
∴$\angle EBC=\angle D$。又$\angle 1=\angle 3$，
∴$\triangle ADB\sim\triangle CBE$，
∴$\frac{AB}{CE}=\frac{AD}{CB}$，
∴$AB\cdot CB = AD\cdot CE$；【探索应用】证明:
∵正方形$ABCD$，
∴$\angle C=\angle D = 90^{\circ}$。
∵$EG\perp GF$，
∴$\angle EGF = 90^{\circ}$，$\angle EGC+\angle FGD = 90^{\circ}$。又$\angle CEG+\angle EGC = 90^{\circ}$，
∴$\angle CEG=\angle FGD$。又$\angle C=\angle D$，
∴$\triangle CEG\sim\triangle DGF$，
∴$\frac{CE}{DG}=\frac{CG}{DF}$，
∴$CE\cdot DF = DG\cdot CG = 4\times2 = 8$，
∴$CE\cdot DF$是定值。【拓展延伸】9