《2025年名师学案九年级数学下册人教版》

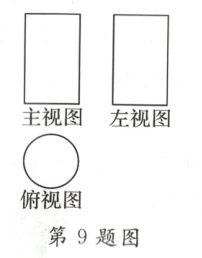
9. 如图图形是某几何体的三视图. 已知主视图和左视图是两个全等的矩形. 若主视图的相邻两边长分别为2和3，俯视图是直径等于2的圆，则这个几何体的体积为______.

答案： $3\pi$

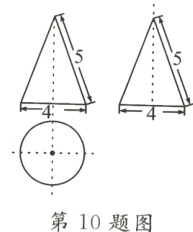
10. 已知某几何体的三视图如图，其中主视图和左视图都是腰长为5，底边长为4的等腰三角形，则该几何体的侧面展开图的面积是________.（结果保留π）

答案： $10\pi$

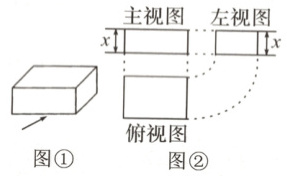
11. 图②是图①中长方体的三视图，若用S表示面积，S主=x²+2x，S左=x²+x，则S俯=______________.

答案： $x^{2}+3x + 2$

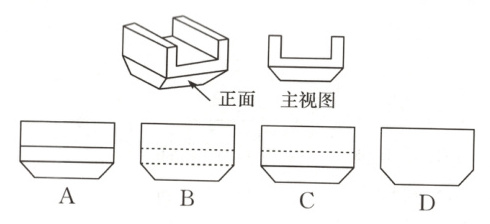
12.【新课标·传统文化】（2024·山西）斗拱是中国古典建筑上的重要部件. 如图是一种斗形构件“三才升”的示意图及其主视图，则它的左视图为（ ）

答案： C

13. 由相同的小正方体搭成的立体图形的部分视图如图所示，则搭成该立体图形的小正方体的最少个数为（ ）

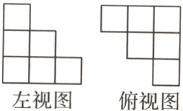
A. 6
B. 9
C. 10
D. 14

答案： B

14.【新课标·传统文化】陕西饮食文化源远流长，“老碗面”是陕西地方特色美食之一. 图②是从正面看到的一个“老碗”（图①）的形状示意图. AB是⊙O的一部分，D是AB的中点，连接OD，与弦AB交于点C，连接OA，OB. 已知AB=24 cm，碗深CD=8 cm，则⊙O的半径OA为________cm.

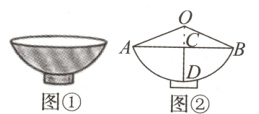
答案： 13

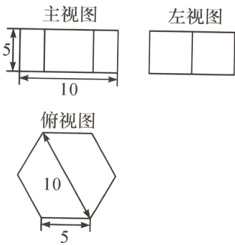
15. 如图是一个包装纸盒的三视图（单位：cm），其中俯视图为正六边形.
（1）该包装纸盒的几何形状是____________；
（2）画出该纸盒的平面展开图；
（3）计算制作一个纸盒所需纸板的面积（精确到1 cm²，$\sqrt{3}$≈1.73）.

答案： 正六棱柱 解：
(2)画图略；
(3)由图可知：正六棱柱的侧面是边长为5 cm的正方形，上、下底面是边长为5 cm的正六边形，侧面积为$6\times5\times5 = 150(cm^{2})$，两个底面积为$2\times6\times\frac{\sqrt{3}}{4}\times5\times5 = 75\sqrt{3}(cm^{2})$，故制作一个纸盒所需纸板的面积为$150 + 75\sqrt{3}\approx280(cm^{2})$. 答：制作一个纸盒所需纸板的面积约为$280cm^{2}$.