《2025年名师学案九年级数学下册人教版》

1. 在Rt△ABC中，∠C = 90°，除直角外的五个元素之间有如下关系：
　　　　　　　
(1)三边之间的关系：____________________；
(2)两锐角之间的关系：__________________；
(3)边角之间的关系：sinA = ________，cosA = ________，tanA = ________.

答案： 1.（1）$a^{2}+b^{2}=c^{2}$ （2）$\angle A+\angle B = 90^{\circ}$ （3）$\frac{a}{c}$ $\frac{b}{c}$ $\frac{a}{b}$

2. 在直角三角形中，由已知元素求出其余未知元素的过程叫做______________.

答案： 解直角三角形

1. (1)如图，在△ABC中，∠C = 90°，AB = 4，AC = 2，欲求∠B的度数，最合适的做法是( )
A. 计算sin B的值求出
B. 计算cos B的值求出
C. 计算tan B的值求出
D. 先根据cos A求出∠A，再用90° - ∠A求出
　　　　　　　　　　　　
(2)【T1(1)变式】在Rt△ABC中，∠C = 90°，AB = 2$\sqrt{5}$，AC = $\sqrt{15}$，则∠A的度数是( )
A. 90° B. 60° C. 45° D. 30°

答案： 1.（1）A （2）D

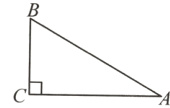
2.【教材P73例1变式】如图，在△ABC中，∠C = 90°，BC = $\sqrt{6}$，AC = 3$\sqrt{2}$，解这个直角三角形.
　　　　　　　　　　　　

答案： 解：在$Rt\triangle ABC$中，$\tan A=\frac{BC}{AC}=\frac{\sqrt{6}}{3\sqrt{2}}=\frac{\sqrt{3}}{3}$，$\therefore\angle A = 30^{\circ}$.$\therefore\angle B = 90^{\circ}-\angle A = 60^{\circ}$.$\because\sin A=\sin 30^{\circ}=\frac{BC}{AB}=\frac{1}{2}$，$\therefore AB = 2BC = 2\sqrt{6}$.$\therefore\angle A = 30^{\circ}$，$\angle B = 60^{\circ}$，$AB = 2\sqrt{6}$.

3. 如图，在△ABC中，∠C = 90°，∠B = 50°，AB = 10，则BC的长为( )
A. 10 tan 50° B. 10 cos 50°
C. 10 sin 50° D. $\frac{10}{cos50°}$
　　　　 　　　

答案： B

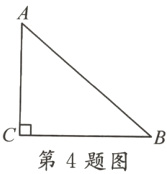
4. 如图，△ABC中，∠C = 90°，AB = 6，cos B = $\frac{2}{3}$，则AC的长是( )


A. 4.5
B. 5
C. 2$\sqrt{5}$
D. 3$\sqrt{5}$

答案： C

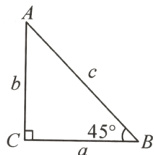
5.【教材P73例2变式】如图，在△ABC中，∠C = 90°，c = 8$\sqrt{2}$，∠B = 45°，解这个直角三角形.
　　　　　　　　　　　　　　

答案： 解：$\because\angle C = 90^{\circ}$，$\angle B = 45^{\circ}$，$\therefore\angle A = 90^{\circ}-\angle B = 45^{\circ}$.$\because\sin B=\frac{b}{c}=\sin 45^{\circ}$，$\therefore b = c\cdot\sin 45^{\circ}=8\sqrt{2}\times\frac{\sqrt{2}}{2}=8$.$\because\tan B=\frac{b}{a}=\tan 45^{\circ}=1$，$\therefore a = b = 8$.$\therefore\angle A = 45^{\circ}$，$a = b = 8$.

6. 在△ABC中，AB = 12$\sqrt{2}$，AC = 13，cos B = $\frac{\sqrt{2}}{2}$，则BC的边长为________.
【点拨】由于△ABC的类型不确定，故分两种情况讨论：①∠ACB是锐角；②∠ACB是钝角. 然后作BC边上的高，结合三角函数的定义和勾股定理解答.

答案： 7或17