第99页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1. 新独家原创 嫦娥六号是中国探月工程第六个探测器,它的最高速度达到31马赫,相当于每秒约10.6千米。下图是4种不同飞船的最高速度,它们的极差是 ( )
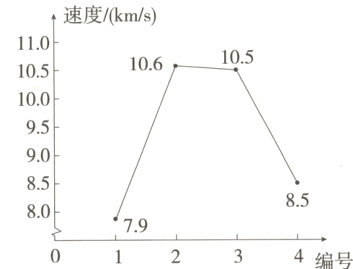
A.0.6
B.0.1
C.2
D.2.7

A.0.6
B.0.1
C.2
D.2.7
答案:
①D 由题图可知,最快速度为10.6 km/s,最慢速度为7.9 km/s,所以极差为10.6 - 7.9 = 2.7. 故选D.
2. (2023北京通州期末)方差的统计含义:表示一组数据的每个数( )
A.偏离它的众数的差的平均值
B.偏离它的平均数的差的绝对值的平均值
C.偏离它的中位数的差的平方数的平均值
D.偏离它的平均数的差的平方数的平均值
A.偏离它的众数的差的平均值
B.偏离它的平均数的差的绝对值的平均值
C.偏离它的中位数的差的平方数的平均值
D.偏离它的平均数的差的平方数的平均值
答案:
②D 方差的统计含义:表示一组数据的每个数偏离它的平均数的差的平方数的平均值. 故选D.
3. (2024山东烟台中考)射击运动队进行射击测试,甲、乙两名选手的测试成绩如下图。其成绩的方差分别记为s²甲和s²乙,则s²甲和s²乙的大小关系是 ( )
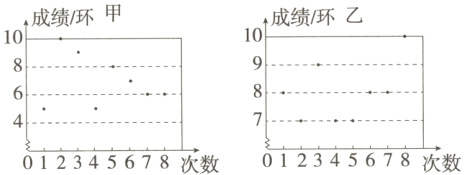
A.s²甲>s²乙
B.s²甲<s²乙
C.s²甲=s²乙
D.无法确定

A.s²甲>s²乙
B.s²甲<s²乙
C.s²甲=s²乙
D.无法确定
答案:
③A 方差体现了一组数据的离散程度,方差越小,数据的波动越小. 由题图可知,乙选手的8次射击成绩相对稳定,
∴$s_{甲}^{2}>s_{乙}^{2}$. 故选A.
∴$s_{甲}^{2}>s_{乙}^{2}$. 故选A.
4. (2021北京中考)有甲、乙两组数据,如下表所示:
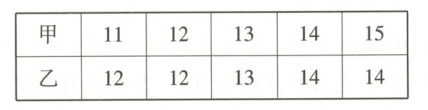
甲、乙两组数据的方差分别为s²甲,s²乙,则s²甲____s²乙(填“>”“<”或“ =”).(M8217001)

甲、乙两组数据的方差分别为s²甲,s²乙,则s²甲____s²乙(填“>”“<”或“ =”).(M8217001)
答案:
④答案 >
解析 $\overline{x}_{甲}=\frac{1}{5}\times(11 + 12 + 13 + 14 + 15)=13$,$s_{甲}^{2}=\frac{1}{5}\times[(11 - 13)^{2}+(12 - 13)^{2}+(13 - 13)^{2}+(14 - 13)^{2}+(15 - 13)^{2}]=2$,$\overline{x}_{乙}=\frac{1}{5}\times(12 + 12 + 13 + 14 + 14)=13$,$s_{乙}^{2}=\frac{1}{5}\times[(12 - 13)^{2}+(12 - 13)^{2}+(13 - 13)^{2}+(14 - 13)^{2}+(14 - 13)^{2}]=0.8$,
∵2>0.8,
∴$s_{甲}^{2}>s_{乙}^{2}$.
解析 $\overline{x}_{甲}=\frac{1}{5}\times(11 + 12 + 13 + 14 + 15)=13$,$s_{甲}^{2}=\frac{1}{5}\times[(11 - 13)^{2}+(12 - 13)^{2}+(13 - 13)^{2}+(14 - 13)^{2}+(15 - 13)^{2}]=2$,$\overline{x}_{乙}=\frac{1}{5}\times(12 + 12 + 13 + 14 + 14)=13$,$s_{乙}^{2}=\frac{1}{5}\times[(12 - 13)^{2}+(12 - 13)^{2}+(13 - 13)^{2}+(14 - 13)^{2}+(14 - 13)^{2}]=0.8$,
∵2>0.8,
∴$s_{甲}^{2}>s_{乙}^{2}$.
5. 教材变式·P123T2 (2024北京西城期末)某果园收获了一批苹果,有2 000个苹果作为大果装入包装盒进行销售。设苹果的果径为x mm,其中A款包装盒中的苹果果径要求是80≤x<85,B款包装盒中的苹果果径要求是85≤x<90。从这2 000个苹果中随机抽取20个,测量它们的果径(单位:mm),所得数据整理如下:
80 81 82 82 83 84 84 85 86 86 87 87 87 89 90 91 92 92 94 98
(1)这20个苹果的果径的众数是________,中位数是________。
(2)如果一个包装盒中苹果果径的方差越小,那么认为该包装盒中的苹果大小越均匀。从抽取的苹果中分别选出6个装入两个包装盒,其果径如表所示(单位:mm)。
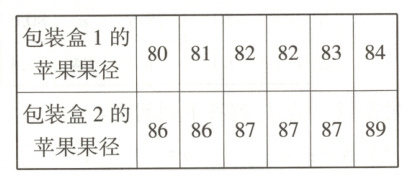
其中,包装盒________中的苹果大小更均匀(填“1”或“2”)。
(3)请估计这2 000个苹果中,符合A款包装盒要求的苹果有多少个。
80 81 82 82 83 84 84 85 86 86 87 87 87 89 90 91 92 92 94 98
(1)这20个苹果的果径的众数是________,中位数是________。
(2)如果一个包装盒中苹果果径的方差越小,那么认为该包装盒中的苹果大小越均匀。从抽取的苹果中分别选出6个装入两个包装盒,其果径如表所示(单位:mm)。

其中,包装盒________中的苹果大小更均匀(填“1”或“2”)。
(3)请估计这2 000个苹果中,符合A款包装盒要求的苹果有多少个。
答案:
⑤解析
(1)这20个数据中,87出现的次数最多,故众数是87.
把20个数据从小到大排列,排在中间的两个数分别是86,87,故中位数是$\frac{86 + 87}{2}=86.5$.
(2)包装盒1的苹果果径的平均数为$\frac{80 + 81 + 82 + 82 + 83 + 84}{6}=82$,
包装盒1的苹果果径的方差为$\frac{1}{6}\times[(80 - 82)^{2}+(81 - 82)^{2}+(82 - 82)^{2}+(82 - 82)^{2}+(83 - 82)^{2}+(84 - 82)^{2}]=\frac{5}{3}$,
包装盒2的苹果果径的平均数为$\frac{86 + 86 + 87 + 87 + 87 + 89}{6}=87$,
包装盒2的苹果果径的方差为$\frac{1}{6}\times[2\times(86 - 87)^{2}+3\times(87 - 87)^{2}+(89 - 87)^{2}]=1$,
因为1<$\frac{5}{3}$,所以包装盒2中的苹果大小更均匀.
(3)满足80≤x<85的数据共7个,
2000×$\frac{7}{20}$ = 700(个).
答:估计符合A款包装盒要求的苹果有700个.
(1)这20个数据中,87出现的次数最多,故众数是87.
把20个数据从小到大排列,排在中间的两个数分别是86,87,故中位数是$\frac{86 + 87}{2}=86.5$.
(2)包装盒1的苹果果径的平均数为$\frac{80 + 81 + 82 + 82 + 83 + 84}{6}=82$,
包装盒1的苹果果径的方差为$\frac{1}{6}\times[(80 - 82)^{2}+(81 - 82)^{2}+(82 - 82)^{2}+(82 - 82)^{2}+(83 - 82)^{2}+(84 - 82)^{2}]=\frac{5}{3}$,
包装盒2的苹果果径的平均数为$\frac{86 + 86 + 87 + 87 + 87 + 89}{6}=87$,
包装盒2的苹果果径的方差为$\frac{1}{6}\times[2\times(86 - 87)^{2}+3\times(87 - 87)^{2}+(89 - 87)^{2}]=1$,
因为1<$\frac{5}{3}$,所以包装盒2中的苹果大小更均匀.
(3)满足80≤x<85的数据共7个,
2000×$\frac{7}{20}$ = 700(个).
答:估计符合A款包装盒要求的苹果有700个.
查看更多完整答案,请扫码查看


