第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
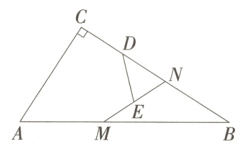
8.(2024北京师大附中期中,7,)如图,在Rt△ABC中,∠C = 90°,AC = 6,BC = 8,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN,MN的中点,则DE的最小值是( )
A.2 B.$\frac{12}{5}$ C.3 D.$\frac{24}{5}$
A.2 B.$\frac{12}{5}$ C.3 D.$\frac{24}{5}$

答案:
B 如图,连接CM,

∵点D、E分别为CN,MN的中点,
∴DE = $\frac{1}{2}$CM,
∴当CM⊥AB时,CM的值最小,此时DE有最小值,
∵∠C = 90°,AC = 6,BC = 8,
∴AB = $\sqrt{AC^{2}+BC^{2}}$=$\sqrt{6^{2}+8^{2}}$= 10,
∴CM = $\frac{\frac{1}{2}AC·BC}{\frac{1}{2}AB}$=$\frac{24}{5}$,
∴DE的最小值是$\frac{12}{5}$.故选B.
B 如图,连接CM,

∵点D、E分别为CN,MN的中点,
∴DE = $\frac{1}{2}$CM,
∴当CM⊥AB时,CM的值最小,此时DE有最小值,
∵∠C = 90°,AC = 6,BC = 8,
∴AB = $\sqrt{AC^{2}+BC^{2}}$=$\sqrt{6^{2}+8^{2}}$= 10,
∴CM = $\frac{\frac{1}{2}AC·BC}{\frac{1}{2}AB}$=$\frac{24}{5}$,
∴DE的最小值是$\frac{12}{5}$.故选B.
9.(2023北京人大附中西山学校月考,8,)如图,点A、B为定点,定直线l//AB,P是l上的一个动点,点M、N分别是PA、PB的中点,在①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小中,会随点P的移动而变化的是( )
A.②③⑤ B.②⑤ C.①③④ D.⑤

A.②③⑤ B.②⑤ C.①③④ D.⑤

答案:
B
∵点M、N分别为PA、PB的中点,
∴MN是△ABP的中位线,
∴MN = $\frac{1}{2}$AB,
∵A、B为定点,
∴线段MN的长不会随点P的移动而变化;
∵PA、PB的长随点P的移动而变化,
∴△PAB的周长随点P的移动而变化;
∵MN//AB,l//AB,
∴MN//l,
∵P是l上的一个动点,
∴点P到MN的距离为定值,
∵MN的长为定值,
∴△PMN的面积为定值,即△PMN的面积不会随点P的移动而变化;
∵MN//AB//l,点P在直线l上,MN是△ABP的中位线,
∴直线MN,AB之间的距离不会随点P的移动而变化;∠APB的大小随点P的移动而变化.
综上,会随点P的移动而变化的是②⑤,故选B.
∵点M、N分别为PA、PB的中点,
∴MN是△ABP的中位线,
∴MN = $\frac{1}{2}$AB,
∵A、B为定点,
∴线段MN的长不会随点P的移动而变化;
∵PA、PB的长随点P的移动而变化,
∴△PAB的周长随点P的移动而变化;
∵MN//AB,l//AB,
∴MN//l,
∵P是l上的一个动点,
∴点P到MN的距离为定值,
∵MN的长为定值,
∴△PMN的面积为定值,即△PMN的面积不会随点P的移动而变化;
∵MN//AB//l,点P在直线l上,MN是△ABP的中位线,
∴直线MN,AB之间的距离不会随点P的移动而变化;∠APB的大小随点P的移动而变化.
综上,会随点P的移动而变化的是②⑤,故选B.
10.新考向·规律探究题 (2024北京人大附中朝阳学校模拟改编,14,)如图,△ABC的周长为16,连接△ABC三边中点构成第一个△A₁B₁C₁,再连接△A₁B₁C₁的各边中点构成第二个△A₂B₂C₂,依此类推,则第2025个三角形的周长为________.


答案:
答案 $\frac{1}{2^{2021}}$
解析
∵△ABC的周长为16,△A₁B₁C₁的三条边为△ABC的三条中位线,
∴第1个三角形的周长为$\frac{1}{2^{1}}$×2⁴;第2个三角形的周长为$\frac{1}{2^{2}}$×2⁴,依此类推,第n个三角形的周长为$\frac{1}{2^{n}}$×2⁴,
∴第2025个三角形的周长为$\frac{1}{2^{2025}}$×2⁴=$\frac{1}{2^{2021}}$.
解析
∵△ABC的周长为16,△A₁B₁C₁的三条边为△ABC的三条中位线,
∴第1个三角形的周长为$\frac{1}{2^{1}}$×2⁴;第2个三角形的周长为$\frac{1}{2^{2}}$×2⁴,依此类推,第n个三角形的周长为$\frac{1}{2^{n}}$×2⁴,
∴第2025个三角形的周长为$\frac{1}{2^{2025}}$×2⁴=$\frac{1}{2^{2021}}$.
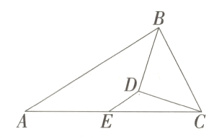
11.(2024北京一六一中学分校期中,16,)如图,△ABC中,AB = 2a + 1,BC = 2a - 3,BD平分∠ABC,过点C作CD⊥BD于点D,E是AC的中点,连接DB,则DE =________.

答案:
答案 2
解析 如图,延长CD交AB于F,
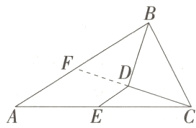
∵BD平分∠ABC,CD⊥BD,
∴△BCF是等腰三角形,
∴BF = BC = 2a - 3,FD = CD,
∵E是AC的中点,
∴DE是△AFC的中位线,
∴DE = $\frac{1}{2}$AF.
∵AF = AB - BF = 2a + 1 - (2a - 3)= 4,
∴DE = 2.
答案 2
解析 如图,延长CD交AB于F,

∵BD平分∠ABC,CD⊥BD,
∴△BCF是等腰三角形,
∴BF = BC = 2a - 3,FD = CD,
∵E是AC的中点,
∴DE是△AFC的中位线,
∴DE = $\frac{1}{2}$AF.
∵AF = AB - BF = 2a + 1 - (2a - 3)= 4,
∴DE = 2.
12.(2023北京清华附中上地学校期中,18,)如图,△ABC中,D、E、F分别是BC、CA、AB的中点,G、M、N分别是线段AE、AF、BD上的点,且GM//BC,GN//AB,GN与EF交于点K,如果四边形FKGM的面积是2,四边形EKND的面积是3,则△GKE的面积是________.


答案:
答案 $\frac{1}{2}$
解析 如图,过A作AQ//BC,延长DE交AQ于Q,延长NG交AQ于P,延长MG交QE于L,

∵D,E,F分别是BC,AC,AB的中点,
∴DE,EF是△ABC的中位线,
∴EQ//FA,EF//BC,
∴EF//AQ,
∴四边形AFEQ是平行四边形,
∵ML//BC,
∴ML//AQ,ML//FE,
∵NP//AB,
∴NP//DQ,
∴四边形AMGP,四边形GKEL是平行四边形,
∴△AFE的面积 = △AQE的面积,△AMG的面积 = △APG的面积,△KGE的面积 = △LGE的面积,
∴平行四边形MFKG的面积 = 平行四边形QPGL的面积 = 2,
∵NK = BF,PK = AF,AF = BF,
∴NK = PK,
∴平行四边形PKEQ的面积 = 平行四边形NDEK的面积 = 3,
∴平行四边形GKEL的面积 = 3 - 2 = 1,
∴△GKE的面积是$\frac{1}{2}$.
答案 $\frac{1}{2}$
解析 如图,过A作AQ//BC,延长DE交AQ于Q,延长NG交AQ于P,延长MG交QE于L,

∵D,E,F分别是BC,AC,AB的中点,
∴DE,EF是△ABC的中位线,
∴EQ//FA,EF//BC,
∴EF//AQ,
∴四边形AFEQ是平行四边形,
∵ML//BC,
∴ML//AQ,ML//FE,
∵NP//AB,
∴NP//DQ,
∴四边形AMGP,四边形GKEL是平行四边形,
∴△AFE的面积 = △AQE的面积,△AMG的面积 = △APG的面积,△KGE的面积 = △LGE的面积,
∴平行四边形MFKG的面积 = 平行四边形QPGL的面积 = 2,
∵NK = BF,PK = AF,AF = BF,
∴NK = PK,
∴平行四边形PKEQ的面积 = 平行四边形NDEK的面积 = 3,
∴平行四边形GKEL的面积 = 3 - 2 = 1,
∴△GKE的面积是$\frac{1}{2}$.
13.(2023北京师大附中期中改编,22,)我们把连接三角形两边中点的线段叫做三角形的中位线.三角形的中位线有如下性质:三角形的中位线平行于三角形的第三边并且等于第三边的一半.如图1,点D,E分别是△ABC的边AB,AC的中点,则DE//BC且DE = $\frac{1}{2}$BC.
如图2,四边形ABCD中,点M是边AB的中点,点N是边CD的中点,若AD//BC,AD = 4,MN = 5,求BC的长.

如图2,四边形ABCD中,点M是边AB的中点,点N是边CD的中点,若AD//BC,AD = 4,MN = 5,求BC的长.

答案:
解析 如图所示,连接AN并延长交BC的延长线于E,

∵AD//BC,
∴∠NAD = ∠NEC,∠NDA = ∠NCE,
∵点N是CD的中点,
∴DN = CN,
在△ADN和△ECN中,$\begin{cases}∠NAD = ∠NEC,\\∠NDA = ∠NCE,\\DN = CN,\end{cases}$
∴△ADN≌△ECN(AAS),
∴CE = AD = 4,AN = NE,即点N是AE的中点,
又
∵点M是AB的中点,
∴BE = 2MN = 10,
∴BC = BE - CE = 10 - 4 = 6.
解析 如图所示,连接AN并延长交BC的延长线于E,

∵AD//BC,
∴∠NAD = ∠NEC,∠NDA = ∠NCE,
∵点N是CD的中点,
∴DN = CN,
在△ADN和△ECN中,$\begin{cases}∠NAD = ∠NEC,\\∠NDA = ∠NCE,\\DN = CN,\end{cases}$
∴△ADN≌△ECN(AAS),
∴CE = AD = 4,AN = NE,即点N是AE的中点,
又
∵点M是AB的中点,
∴BE = 2MN = 10,
∴BC = BE - CE = 10 - 4 = 6.
查看更多完整答案,请扫码查看


