《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

1.(2023北京大兴期末)从一块正方形的木板上锯掉2 m宽的长方形木条,剩下的木板的面积是48 m²,则原来这块木板的面积是( )
A.100 m²
B.64 m²
C.121 m²
D.144 m²

答案： B 设原来这块木板的边长为x m.由题意，可知x(x - 2)=48，解得x₁ = 8，x₂ = -6(不合题意，舍去)，所以原来这块木板的边长为8 m，面积为8×8 = 64(m²). 故选B.

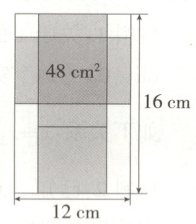
2.(2024重庆渝中巴蜀中学期中)如图,在劳动技能课程中,小张同学将一张长16 cm,宽12 cm的矩形纸板,剪去两个全等的正方形和两个全等的矩形后,剩余部分恰好制作成底面积为48 cm²的有盖长方体工艺盒,则剪去的正方形的边长为 ( )


A.1.5 cm
B.2 cm
C.2.5 cm
D.3 cm

答案： B 设剪去的正方形的边长为x cm，依题意得(12 - 2x)·$\frac{16 - 2x}{2}$ = 48，整理得x² - 14x + 24 = 0，解得x₁ = 2，x₂ = 12(不符合题意，舍去).
∴剪去的正方形的边长为2 cm.故选B.

3.教材变式·P108例1某农场要建一个饲养场(矩形ABCD),其中两面利用现有的墙(AD位置的墙最大可用长度为27米,AB位置的墙最大可用长度为15米),另两面用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏).建成后木栏总长45米.若饲养场的面积为180平方米,则饲养场(矩形ABCD)的边AB的长为______米.

答案： 答案 10 解析 设饲养场(矩形ABCD)的边AB的长为x米，则BC = 45 + 3 - 3x = (48 - 3x)米，根据题意得x(48 - 3x)=180，解得x₁ = 6，x₂ = 10，
∵0＜48 - 3x≤27，0＜x≤15，
∴7≤x≤15，
∴x = 10.故饲养场(矩形ABCD)的边AB的长为10米.

4.新考向·项目式学习试题综合与实践:如何用最少的材料设计花园?
【问题情境】如图,小王打算用篱笆围一个矩形花园ABCD,其中一边靠墙,墙长为10米,现可用的篱笆总长为20米,设AB的长为x米.
【项目解决】
目标1:确定面积与边长的关系.
当篱笆全部用完,且围成矩形花园ABCD的面积为32平方米时,求BC的长.
目标2:探究最少的材料方案.
现要围面积为$\frac{81}{2}$平方米的矩形花园,设所用的篱笆为m米.
(1)若m = 14,能成功围成吗?若能,求出AB的长;若不能,请说明理由.
(2)若要成功围成,则m的最小值为______,此时AB = ______米.

答案： 解析 目标1：
∵可用的篱笆总长为20米，且AB的长为x米，
∴BC的长为(20 - 2x)米.根据题意得x(20 - 2x)=32，整理得x² - 10x + 16 = 0，解得x₁ = 2，x₂ = 8，当x = 2时，20 - 2x = 20 - 2×2 = 16＞10，不符合题意；当x = 8时，20 - 2x = 20 - 2×8 = 4＜10，符合题意.答：BC的长为4米.目标2：
(1)不能围成面积为$\frac{81}{2}$平方米的矩形花园，理由：假设能围成面积为$\frac{81}{2}$平方米的矩形花园，设AB的长为y米，则BC的长为(14 - 2y)米，根据题意得y(14 - 2y)=$\frac{81}{2}$，整理得4y² - 28y + 81 = 0，
∵Δ = (-28)² - 4×4×81 = -512＜0，
∴原方程没有实数根，
∴假设不成立，即不能围成面积为$\frac{81}{2}$平方米的矩形花园.
(2)18；$\frac{9}{2}$. 详解：设AB的长为a米，则BC的长为(m - 2a)米，根据题意得a(m - 2a)=$\frac{81}{2}$，整理得4a² - 2ma + 81 = 0，若要成功围成，则方程有实数根，
∴Δ = (-2m)² - 4×4×81≥0，
∴m≥18或m≤ -18(不符合题意，舍去)，
∴m的最小值为18.当m = 18时，原方程为4a² - 36a + 81 = 0，解得a₁ = a₂ = $\frac{9}{2}$，当a = $\frac{9}{2}$时，18 - 2a = 18 - 2×$\frac{9}{2}$ = 9＜10，符合题意，
∴AB = $\frac{9}{2}$米.