《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

17. (2024河北邯郸育华实验学校模拟,20,)已知n边形的内角和θ = (n - 2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由.
(2)若n边形变为(n + x)边形,发现内角和增加了540°,用列方程的方法确定x.

答案： 解析
(1)甲的说法对，乙的说法不对，理由：
360°÷180° = 2，630°÷180° = 3……90°，
∵边数n为整数，
∴甲的说法对，乙的说法不对，n = 360°÷180° + 2 = 2 + 2 = 4.
(2)依题意得(n + x - 2)×180°-(n - 2)×180° = 540°，
解得x = 3.

18. 新考向·项目式学习试题(2024山东潍坊潍城期末,20,)某校数学兴趣小组为了研究多边形中从一个顶点出发可以作几条对角线，以及该多边形中对角线的总条数与边数的关系，他们决定从以下图形开始寻找规律.


(1)请在图5中画出从A点出发的所有对角线.
(2)根据探究,整理得到下面表格:

表格中a = _______,b = _______.(用含n的代数式表示)
(3)拓展应用:若该校要举办足球比赛,总共有9个班级参加比赛,规定每个班级都要和其他班级比赛一次.请问总共要比赛多少场.

答案：
解析
(1)如图所示.

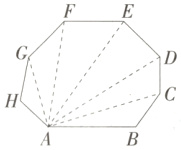
(2)由题表可得a = n - 3，
多边形对角线的总条数=$\frac{n(n - 3)}{2}$，
∴b=$\frac{n(n - 3)}{2}$.故答案为n - 3；$\frac{n(n - 3)}{2}$.
(3)$\frac{9×(9 - 1)}{2}$ = 36(场).
答:总共要比赛36场.

19. 模型观念(2024重庆万州期末)两个多边形,一个多边形记为A,另一个多边形记为B,多边形A的边数是多边形B的边数的2倍.
(1)若多边形A的内角和是多边形B的内角和的3倍,求多边形A和多边形B的边数.
(2)利用边长相等的A型正多边形瓷砖和B型正多边形瓷砖能够镶嵌(不重叠、无缝隙地密铺)地面,在一个顶点的周围有a块A型正多边形瓷砖和b块B型正多边形瓷砖(ab ≠ 0),求a + b的值.

答案： 解析
(1)设多边形B的边数为n，则多边形A的边数是2n，由题意得(2n - 2)×180° = 3×(n - 2)×180°，
解得n = 4，
∴2n = 2×4 = 8，
∴多边形A的边数是8，多边形B的边数是4.
(2)
∵ab≠0，
∴a≠0，b≠0，
∵正四边形和正八边形的每个内角分别为90°，135°，
由题意得135a + 90b = 360，
∴3a + 2b = 8，
∵a、b为整数，
∴a = 2，b = 1，
∴a + b = 2 + 1 = 3.