《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

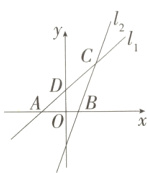
20. [答案含评分细则](2024北京清华附中期中)(10分)如图,在平面直角坐标系xOy中,直线$l_{1}$:y = x + 2与x轴交于点A,与y轴交于点D,直线$l_{2}$与x轴交于点B(1,0),与直线$l_{1}$相交于点C(m,4).
(1)求直线$l_{2}$的表达式.
(2)求四边形OBCD的面积.
(3)若点M为x轴上一动点,过点M(t,0)作垂直于x轴的直线,与直线$l_{2}$交于点Q.若$S_{△AQC}=2S_{△ABC}$,请直接写出所有符合要求的点Q的坐标.

答案： 解析　
(1)
∵直线y = x + 2与直线l₂相交于点C(m，4),
∴4 = m + 2,解得m = 2,
∴C(2,4),　　　　　　　1分
设直线l₂的表达式为y = kx + b(k≠0),
把B(1,0),C(2,4)代入得
$\begin{cases}0 = k + b\\4 = 2k + b\end{cases}$,解得$\begin{cases}k = 4\\b = - 4\end{cases}$,　　　　　　　　　　　3分
∴直线l₂的表达式为y = 4x - 4.　　　　　　　　4分
(2)对于y = x + 2,当x = 0时,y = 2,
∴D(0,2),
∴OD = 2,　　　　　　　　　　　　　　　　　5分
当y = 0时,x = - 2,
∴A(-2,0),
∴OA = 2,　　　　　　　　　　　　　　　　　6分
∵B(1,0),
∴AB = 3,
∴S四边形OBCD = S△ABC - S△AOD
=$\frac{1}{2}$×3×4 - $\frac{1}{2}$×2×2 = 4.　　　　　　　　　　　8分
(3)点Q的坐标为(0,−4)或(4,12).　　　　　10分
详解:
∵M(t,0),MQ⊥x轴,点Q在直线l₂上,
∴Q(t,4t - 4),
∵S△ABC = $\frac{1}{2}$×3×4 = 6,
∴S△AQC = 2S△ABC = 12,
当点Q在点C的上方时，
S△AQC = S△ABQ - S△ABC = $\frac{1}{2}$×3(4t - 4)-6 = 12,
解得t = 4,
∴此时点Q的坐标为(4,12);
当点Q在点C的下方时，
S△AQC = $\frac{1}{2}$×3(4 - 4t + 4)=12,
解得t = 0,
∴此时点Q的坐标为(0,−4).
综上,点Q的坐标为(0,−4)或(4,12).

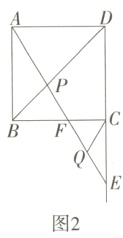
21. [答案含评分细则](2023北京昌平期末)(10分)正方形ABCD中,点E为射线DC上一点(点E不与D,C重合),射线AE交BD于点P,交直线BC于点F,点Q为EF的中点,连接PC,CQ.
(1)如图1,当点E在线段DC上时,写出∠PCQ的度数,并证明.
(2)如图2,当点E在线段DC的延长线上时,过点D作BD的垂线,交直线CQ于点M.
①依题意补全图形.
②用等式表示线段DP,DC,DM的数量关系,并证明.

答案：
解析　
(1)∠PCQ = 90°.
证明:
∵四边形ABCD是正方形，
∴∠ADB = ∠CDB = 45°,DA = DC,
在△DAP和△DCP中，$\begin{cases}DA = DC\\∠ADP = ∠CDP\\DP = DP\end{cases}$,
∴△DAP≌△DCP(SAS),
∴∠DAP = ∠DCP,
∵点Q为EF的中点,∠ECF = 90°,
∴EQ = FQ = CQ,
∴∠QEC = ∠QCE,∠QCF = ∠QFC,
∵∠QEC = ∠DEA,AD//BC,
∴∠DEA = ∠QCE,∠DAE = ∠QFC = ∠DCP,
∵∠DAE + ∠DEA = 90°,
∴∠DCP + ∠QCE = 90°,
∴∠PCQ = 90°.　　　　　　　　　　　　　　　4分
(2)①补全的图形如图.

②DP + DM = $\sqrt{2}$DC.
证明:
∵BD是正方形ABCD的对角线，
∴∠ABD = ∠BDC = 45°,AB = CD,
∵DM⊥BD,
∴∠BDM = 90°,
∴∠CDM = 45°,
∴∠ABP = ∠CDM,
∵AB//DC,
∴∠BAP = ∠CEQ,
由
(1)知∠CEQ = ∠ECQ = ∠DCM,
∴∠BAP = ∠DCM,
∴△BAP≌△DCM(ASA),
∴BP = DM,
∴DP + DM = DP + BP = BD = $\sqrt{2}$DC,
∴DP + DM = $\sqrt{2}$DC.　　　　　　　　　　　　　10分