《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

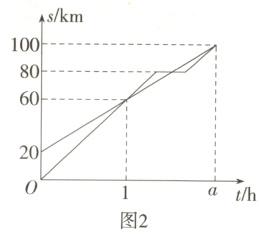
18. [答案含评分细则](2023浙江宁波中考)(8分)某校与部队联合开展红色之旅研学活动,上午7:00,部队官兵乘坐军车从营地出发,同时学校师生乘坐大巴从学校出发,沿公路(如图1)到爱国主义教育基地进行研学.上午8:00,军车在离营地60 km的地方追上大巴并继续前行,到达仓库后,部队官兵下车领取研学物资,然后乘坐军车按原速前行,最后和师生同时到达基地.军车和大巴离营地的路程s(km)与所用时间t(h)的函数关系如图2所示.
(1)求大巴离营地的路程s与所用时间t的函数表达式及a的值.
(2)求部队官兵在仓库领取物资所用的时间.

答案： 解析　
(1)由函数图象可得,大巴的速度为$\frac{60 - 20}{1}$=40(km/h),
∴s = 20 + 40t,
当s = 100时,100 = 20 + 40t,解得t = 2,
∴a = 2,
∴大巴离营地的路程s与所用时间t的函数表达式为s = 20 + 40t,a的值为2.　　　　　　　　　　4分
(2)由函数图象可得,军车的速度为60÷1 = 60(km/h),
设部队官兵在仓库领取物资所用的时间为xh，
根据题意得60(2 - x)=100,解得x = $\frac{1}{3}$,
∴部队官兵在仓库领取物资所用的时间为$\frac{1}{3}$h.

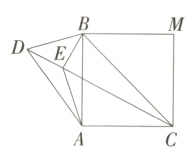
19. [答案含评分细则](2024北京大兴期末)(8分)已知:如图,四边形ABMC是正方形,AD = AC,∠BAD = α(0°＜α＜90°),连接DB,DC,BC.
(1)求∠CDB的度数.
(2)作BE⊥CD于点E,连接AE,用等式表示线段AE,BD,CD之间的数量关系,并证明.

答案：
解析　
(1)
∵四边形ABMC是正方形,AD = AC，
∴AB = AC = AD,
∵∠BAD = α,
∴∠ADB = ∠ABD = $\frac{180° - α}{2}$=90° - $\frac{α}{2}$,　　　　　2分
∵∠BAC = 90°,
∴∠DAC = 90° + α,
∴∠ADC = ∠ACD = $\frac{1}{2}$[180° - (90° + α)]=45° - $\frac{α}{2}$,
∴∠CDB = ∠ADB - ∠ADC = 90° - $\frac{α}{2}$-(45° - $\frac{α}{2}$)=45°.
(2)CD = $\sqrt{2}$BD + $\sqrt{2}$AE.　　　　　　　　　　　　5分
证明:如图,作AF⊥AE交CD于点F,

∴∠EAF = 90°,
∴∠EAB + ∠BAF = ∠FAC + ∠BAF = 90°,
∴∠EAB = ∠FAC,
∵BE⊥CD,∠BDC = 45°,
∴∠DBE = 45°,BE = DE = $\frac{\sqrt{2}}{2}$BD,
∴∠ABE = ∠ABD - 45° = 90° - $\frac{α}{2}$-45° = 45° - $\frac{α}{2}$=∠ACD,
∵AB = AC,
∴ △ABE≌△ACF(ASA),　　　　　7分
∴AE = AF,BE = CF,
∴△AEF是等腰直角三角形,
∴EF = $\sqrt{2}$AE,
∵CD = DE + EF + CF = DE + EF + BE = 2DE + EF = $\sqrt{2}$BD + $\sqrt{2}$AE.　　　　　　　　　　　　　　　　　　　8分