《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

1. (2024辽宁沈阳和平调研)若直线$y = kx + b$经过第一、二、四象限，则函数$y = bx - k$的大致图象是（ ）

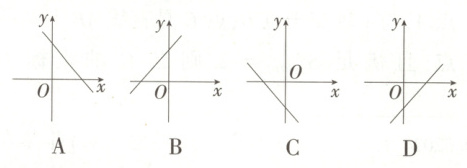
答案： 1 B
∵一次函数y = kx + b的图象经过第一、二、四象限，
∴k＜0，b＞0，
∴ - k＞0，
∴一次函数y = bx - k的图象经过第一、二、三象限. 故选B.

2. (2024陕西西安高新区模拟)直线$l_1:y = kx - b$和$l_2:y = -2kx + b$在同一直角坐标系中的位置可能是（ ）
　　
　

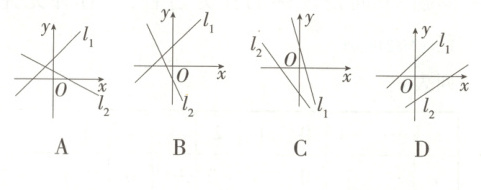
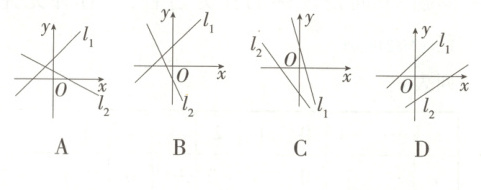
答案： 2 B A.直线l1:y = kx - b中k＞0，b＜0，直线l2:y = - 2kx + b中k＞0，b＞0，b的取值矛盾，故本选项不符合题意；
B.直线l1:y = kx - b中k＞0，b＜0，直线l2:y = - 2kx + b中k＞0，b＜0，k、b的取值范围一致，故本选项符合题意；
C.直线l1:y = kx - b中k＜0，b＜0，直线l2:y = - 2kx + b中k＞0，b＜0，k的取值矛盾，故本选项不符合题意；
D.直线l1:y = kx - b中k＞0，b＜0，直线l2:y = - 2kx + b中k＜0，b＜0，k的取值矛盾，故本选项不符合题意.

15. 推理能力 新考向·新定义试题(2023北京十三中分校期中)我们规定:在平面直角坐标系$xOy$中，如果点$P$到原点$O$的距离为$a$，点$M$到点$P$的距离是$a$的$k(k$为整数)倍，那么点$M$就是点$P$的$k$倍关联点.当点$P_1$的坐标为$(-1.5,0)$时.
(1)如果点$P_1$的2倍关联点$M$在$x$轴上，求出点$M$的坐标.
(2)如果点$M(x,y)$是点$P_1$的$k$倍关联点，且满足$x = -1.5$，$-3\leq y\leq5$，求出$k$的最大值.
　　　　

答案： 解析
(1)设M(m,0)，根据题意可得|m + 1.5| = 2×1.5，解得m = 1.5或m = - 4.5，
∴M(1.5,0)或( - 4.5,0).
(2)
∵P的坐标为( - 1.5,0)且M的横坐标为 - 1.5，
∴M和P在直线x = - 1.5上，
∵ - 3≤y≤5且k为整数，
∴当y = 4.5时，k的值最大，
∴4.5 = 1.5k，解得k = 3.