第88页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
11.(2024北京顺义牛栏山一中实验学校月考,26,★★☆)某芯片公司引进了一条内存芯片生产线,开工第一季度生产200万个,第三季度生产288万个.试回答下列问题:
(1)已知每季度生产量的平均增长率相等,求前三季度生产量的平均增长率.
(2)经调查发现,1条生产线最大产能是600万个/季度,若每增加1条生产线,每条生产线的最大产能将减少20万个/季度,现该公司要保证每季度生产内存芯片2600万个,在增加产能的同时又要节省投入成本(生产线越多,投入成本越大),应该再增加几条生产线?
(1)已知每季度生产量的平均增长率相等,求前三季度生产量的平均增长率.
(2)经调查发现,1条生产线最大产能是600万个/季度,若每增加1条生产线,每条生产线的最大产能将减少20万个/季度,现该公司要保证每季度生产内存芯片2600万个,在增加产能的同时又要节省投入成本(生产线越多,投入成本越大),应该再增加几条生产线?
答案:
解析
(1)设前三季度生产量的平均增长率为x,
依题意得200(1 + x)^{2}=288,
解得x_{1}=0.2 = 20%,x_{2}=-2.2(不符合题意,舍去).
答:前三季度生产量的平均增长率为20%.
(2)设应该再增加m条生产线,则每条生产线的最大产能为(600 - 20m)万个/季度,
依题意得(m + 1)(600 - 20m)=2600,
整理得m^{2}-29m + 100 = 0,
解得m_{1}=4,m_{2}=25,
又
∵在增加产能同时又要节省投入成本,
∴m = 4.
答:应该再增加4条生产线.
(1)设前三季度生产量的平均增长率为x,
依题意得200(1 + x)^{2}=288,
解得x_{1}=0.2 = 20%,x_{2}=-2.2(不符合题意,舍去).
答:前三季度生产量的平均增长率为20%.
(2)设应该再增加m条生产线,则每条生产线的最大产能为(600 - 20m)万个/季度,
依题意得(m + 1)(600 - 20m)=2600,
整理得m^{2}-29m + 100 = 0,
解得m_{1}=4,m_{2}=25,
又
∵在增加产能同时又要节省投入成本,
∴m = 4.
答:应该再增加4条生产线.
12.新考向·项目式学习试题 应用意识 (2024江苏南通期末)【综合与实践】
任务主题:某校数学活动小组探究“西瓜购买、销售方案的选择”.
数据信息:A超市和B水果店售卖同品种西瓜.
信息1:A超市西瓜的售价为4元/千克,无论购买多少均不打折.
信息2:B水果店西瓜的售价为5元/千克,若一次购买3千克以上,超过3千克的部分打折销售.
信息3:B水果店销售西瓜的部分小票统计如下表(精确到1千克).
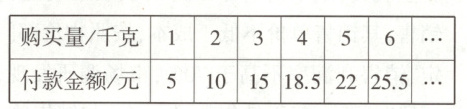
问题解决:
任务1:请直接写出分别在A超市与B水果店购买西瓜的付款金额y(元)与购买量x(千克)之间的函数关系式.
任务2:某酒店承办活动需购买一批西瓜,请通过计算说明选择哪家更划算.
任务3:已知西瓜的进货成本为3元/千克,市场调研发现:如果A超市以4元/千克销售,平均每天可以售出200千克.为了减少库存,超市决定降价销售,根据近期销售情况发现,销售单价每降低0.1元,销售量就会增加20千克,在尽可能减少库存的情况下,该超市将西瓜的销售单价定为多少元时,每天销售西瓜的利润为168元?
任务主题:某校数学活动小组探究“西瓜购买、销售方案的选择”.
数据信息:A超市和B水果店售卖同品种西瓜.
信息1:A超市西瓜的售价为4元/千克,无论购买多少均不打折.
信息2:B水果店西瓜的售价为5元/千克,若一次购买3千克以上,超过3千克的部分打折销售.
信息3:B水果店销售西瓜的部分小票统计如下表(精确到1千克).

问题解决:
任务1:请直接写出分别在A超市与B水果店购买西瓜的付款金额y(元)与购买量x(千克)之间的函数关系式.
任务2:某酒店承办活动需购买一批西瓜,请通过计算说明选择哪家更划算.
任务3:已知西瓜的进货成本为3元/千克,市场调研发现:如果A超市以4元/千克销售,平均每天可以售出200千克.为了减少库存,超市决定降价销售,根据近期销售情况发现,销售单价每降低0.1元,销售量就会增加20千克,在尽可能减少库存的情况下,该超市将西瓜的销售单价定为多少元时,每天销售西瓜的利润为168元?
答案:
解析 任务1:由题意得A超市$:y_{1}=4x.$
B水果店:当0<x≤3时$,y_{2}=5x;$
当x>3时,设$y_{2}$与x之间的函数关系式为$y_{2}=kx + b(k≠0),$
将(4,18.5),(5,22)代入得$\begin{cases}4k + b = 18.5\\5k + b = 22\end{cases},$
∴$\begin{cases}k = 3.5\\b = 4.5\end{cases},$
∴当x>3时$,y_{2}=3.5x + 4.5.$
∴B水果店$:y_{2}=\begin{cases}5x(0<x≤3)\\3.5x + 4.5(x>3)\end{cases}.$
任务2:
∵4x<5x,
∴当0<x≤3时,选择A超市更划算;
令4x = 3.5x + 4.5,解得x = 9,
当3<x<9时,4x<3.5x + 4.5,
∴选择A超市更划算;
当x = 9时,4x = 3.5x + 4.5,
∴选择A超市和B水果店付款金额相同;
当x>9时,4x>3.5x + 4.5,
∴选择B水果店更划算.
综上,当0<x<9时,选择A超市更划算;当x = 9时,选择A超市和B水果店付款金额相同;当x>9时,选择B水果店更划算.
任务3:设该超市西瓜的销售单价为m元,
∴$(m - 3)(200 + 20×\frac{4 - m}{0.1})=168.$
解得$m_{1}=3.6,m_{2}=4.4($舍去).
∴该超市将西瓜的销售单价定为3.6元时,每天销售西瓜的利润为168元.
B水果店:当0<x≤3时$,y_{2}=5x;$
当x>3时,设$y_{2}$与x之间的函数关系式为$y_{2}=kx + b(k≠0),$
将(4,18.5),(5,22)代入得$\begin{cases}4k + b = 18.5\\5k + b = 22\end{cases},$
∴$\begin{cases}k = 3.5\\b = 4.5\end{cases},$
∴当x>3时$,y_{2}=3.5x + 4.5.$
∴B水果店$:y_{2}=\begin{cases}5x(0<x≤3)\\3.5x + 4.5(x>3)\end{cases}.$
任务2:
∵4x<5x,
∴当0<x≤3时,选择A超市更划算;
令4x = 3.5x + 4.5,解得x = 9,
当3<x<9时,4x<3.5x + 4.5,
∴选择A超市更划算;
当x = 9时,4x = 3.5x + 4.5,
∴选择A超市和B水果店付款金额相同;
当x>9时,4x>3.5x + 4.5,
∴选择B水果店更划算.
综上,当0<x<9时,选择A超市更划算;当x = 9时,选择A超市和B水果店付款金额相同;当x>9时,选择B水果店更划算.
任务3:设该超市西瓜的销售单价为m元,
∴$(m - 3)(200 + 20×\frac{4 - m}{0.1})=168.$
解得$m_{1}=3.6,m_{2}=4.4($舍去).
∴该超市将西瓜的销售单价定为3.6元时,每天销售西瓜的利润为168元.
查看更多完整答案,请扫码查看


