《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

8.教材变式·P20例2 (2024山西晋城高平月考)甲、乙两地打电话需付的电话费y(元)是随通话时间t(分钟)的变化而变化的,试根据下表列出的几组数据回答下列问题:(M8214004)
　
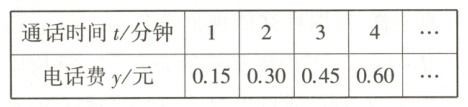
　(1)自变量是__________,因变量是__________.
　(2)写出电话费y(元)与通话时间t(分钟)之间的关系式.
　(3)若小明通话15分钟,则需付电话费多少元？
　(4)若小明某次通话后,需付电话费7.5元,则小明通话多少分钟？

答案： 解析
(1)由题意得,自变量是t,因变量是y,
(2)由题意得,每通话1分钟需付话费0.15元,
∴ 电话费y(元)与通话时间t(分钟)之间的关系式是y = 0.15t.
(3)当t = 15时,y = 0.15×15 = 2.25,故小明通话15分钟,需付电话费2.25元.
(4)当y = 7.5时,0.15t = 7.5,解得t = 50,故小明通话50分钟.

9.(2024广东佛山南海实验中学月考改编)一种圆环(如图所示),它的外圆直径是8厘米,环宽1厘米.(M8214004)
　　　
　(1)如果把这样的2个圆环扣在一起并拉紧(如图2),长度为__________厘米.
　(2)如果把这样的x个圆环扣在一起并拉紧，长度为y厘米,那么y与x之间的关系式是什么？
(3)至少多少个这样的圆环扣在一起并拉紧的长度大于2025厘米？为什么？

答案： 解析
(1)由题意得,把这样的2个圆环扣在一起并拉紧的长度为2×8 - 2 = 16 - 2 = 14(厘米).
(2)把这样的3个圆环扣在一起并拉紧的长度为3×8 - 2×2 = 20(厘米),把这样的4个圆环扣在一起并拉紧的长度为4×8 - 2×3 = 26(厘米),把这样的5个圆环扣在一起并拉紧的长度为5×8 - 2×4 = 32(厘米),……,把这样的x个圆环扣在一起并拉紧的长度为8x - 2(x - 1) = (6x + 2)厘米,
∴ y与x之间的关系式是y = 6x + 2.
(3)至少338个这样的圆环扣在一起并拉紧的长度大于2 025厘米,理由:令6x + 2 = 2 025,解得x = $\frac{2 023}{6}$ = 337……1,
∵ 圆环的个数为整数,
∴ 至少338个这样的圆环扣在一起并拉紧的长度大于2 025厘米.

10.(2023北京人大附中朝阳学校期中,5,★☆☆)下列变量之间的关系中，一个变量是另一个变量的正比例函数的是　　　　　　　　　　　(　　　)
　
A.正方形的面积S随边长x的变化而变化
B.面积为20的三角形的一边上的高h随着这条边的长a的变化而变化　
C.正方形的周长C随着边长x的变化而变化
D.水箱以0.5L/min的流量往外放水,水箱中的剩余水量V(单位:L)随着放水时间t(单位:min)的变化而变化

答案： C 选项A,S = x²,不是一次函数;选项B,h = $\frac{40}{a}$,其中$\frac{40}{a}$不是整式,故不是一次函数;选项C,C = 4x,是正比例函数;选项D,设水箱原来有水x L,由题意知,x是常量,则V = x - 0.5t,是一次函数,不是正比例函数.故选C.

11.(2024山东济南槐荫模拟,8,★☆☆)某农户想要用栅栏围成一个长方形鸡场,如图,鸡场的一边靠墙,另外三边用栅栏围成，若栅栏的总长为20m,设长方形垂直于墙的一边长为xm,面积为y㎡,当x在一定范围内变化时,y随x的变化而变化,则y与x满足的函数关系式是　　　　　　　　　　　(　　　)

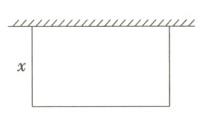
A.y=20x　　　　　　B.y=20−2　
C.y=$\frac{20}{x}$　　　　　　　D.y=x(20−2x)

答案： D
∵ 长方形垂直于墙的一边长为x m,
∴ 平行于墙的一边长为(20 - 2x)m,
∴ y = x(20 - 2x).