《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

9.（2024北京通州期中）已知一次函数y = kx + b的图象经过点A(0,1)，B(2,3).
(1)求这个一次函数的表达式.
(2)在平面直角坐标系xOy中，画出这个函数的图象.

答案：
9 解析
(1)
∵一次函数y = kx + b的图象经过点A(0,1)，B(2,3)，
∴$\begin{cases}b = 1\\2k + b = 3\end{cases}$，解得$\begin{cases}k = 1\\b = 1\end{cases}$，
∴一次函数的表达式为y = x + 1.
(2)一次函数的图象如图.

10.（2023湖北鄂州中考,7,★☆☆）象棋起源于中国，中国象棋文化历史悠久.如图所示的是某次对弈的残图，如果建立平面直角坐标系，使棋子“帅”位于点(-2,-1)的位置，则在同一坐标系下，图象经过棋子“帅”和“马”所在的点的一次函数表达式为（M8214004）（ ）

A.y = x + 1　　　　　　B.y = x - 1
C.y = 2x + 1　　　　　　D.y = 2x - 1

答案： 10 A
∵“帅”位于点(-2,-1)，
∴“马”位于点(1,2)，设图象经过棋子“帅”和“马”所在的点的一次函数的表达式为y = kx + b(k≠0)，
∴$\begin{cases}-1 = -2k + b\\2 = k + b\end{cases}$，解得$\begin{cases}k = 1\\b = 1\end{cases}$，
∴一次函数的表达式为y = x + 1.

11.（2024北京房山期中,8,★★☆）一个一次函数的图象经过点A(0,-3)，且和x轴交于点B，如果该函数图象与坐标轴围成的三角形的面积为6，那么该一次函数的表达式为（ ）
A.y = $\frac{3}{4}$x - 3
B.y = $\frac{3}{2}$x - 3
C.y = $\frac{3}{4}$x - 3或y = -$\frac{3}{4}$x - 3
D.y = $\frac{3}{2}$x - 3或y = -$\frac{3}{2}$x - 3

答案： 11 C 设一次函数的表达式为y = kx + b(k≠0)，
∵$\frac{1}{2}$×3OB = 6，
∴OB = 4，
∴B的坐标为(4,0)或(-4,0)，
∵一次函数的图象经过点A(0,-3)，
∴b = -3，当一次函数图象过点(0,-3)，(4,0)时，4k - 3 = 0，解得k=$\frac{3}{4}$，此时一次函数的表达式为y=$\frac{3}{4}$x - 3；当一次函数图象过点(0,-3)，(-4,0)时，-4k - 3 = 0，解得k = -$\frac{3}{4}$，此时一次函数的表达式为y = -$\frac{3}{4}$x - 3.综上，一次函数表达式为y=$\frac{3}{4}$x - 3或y = -$\frac{3}{4}$x - 3.

12.（2024北京海淀首都师大附中,13,★★☆）对于函数y = kx + b，下表中给出3组自变量和相应的函数值.

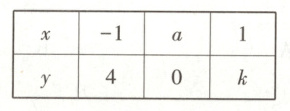
则a + k的值为________.

答案： 12 答案 -4
解析 把x = 1，y = k代入y = kx + b，得k = k + b，解得b = 0，
∴y = kx，把x = -1，y = 4代入y = kx，得4 = -k，
∴k = -4，把x = a，y = 0代入y = -4x，得0 = -4a，
∴a = 0，
∴a + k = -4.

13.（2024四川德阳模拟,16,★★☆）在一次数学探索活动中，老师带领同学们研究了一次函数y = kx + b的系数k,b与图象的关系.为了更直观地理解这一关系，老师给出了直角坐标系中的三个特殊点：A(0,2)，B(2,3)，C(3,1)，要求同学们尝试画出经过这三个点中任意两个点的一次函数图象.同学们通过计算得到了三个一次函数的表达式：y₁ = k₁x + b₁，y₂ = k₂x + b₂，y₃ = k₃x + b₃.接着，老师提出了一个有趣的问题：分别探究k₁ + b₁，k₂ + b₂，k₃ + b₃的值，其中最大的值等于________.

答案： 13 答案 5
解析 设直线AB的表达式为$y_{1}=k_{1}x + b_{1}$，将点A(0,2)，B(2,3)代入得$\begin{cases}b_{1}=2\\2k_{1}+b_{1}=3\end{cases}$，解得$\begin{cases}k_{1}=\frac{1}{2}\\b_{1}=2\end{cases}$，
∴$k_{1}+b_{1}=\frac{5}{2}$.
设直线AC的表达式为$y_{2}=k_{2}x + b_{2}$，将点A(0,2)，C(3,1)代入得$\begin{cases}b_{2}=2\\3k_{2}+b_{2}=1\end{cases}$，解得$\begin{cases}k_{2}=-\frac{1}{3}\\b_{2}=2\end{cases}$，
∴$k_{2}+b_{2}=\frac{5}{3}$.
设直线BC的表达式为$y_{3}=k_{3}x + b_{3}$，将点B(2,3)，C(3,1)代入得$\begin{cases}2k_{3}+b_{3}=3\\3k_{3}+b_{3}=1\end{cases}$，解得$\begin{cases}k_{3}=-2\\b_{3}=7\end{cases}$，
∴$k_{3}+b_{3}=5$，
∴$k_{1}+b_{1}$，$k_{2}+b_{2}$，$k_{3}+b_{3}$中最大的值为5.