《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

9. 新独家原创下列生活中的例子,不属于利用四边形的不稳定性的是( )

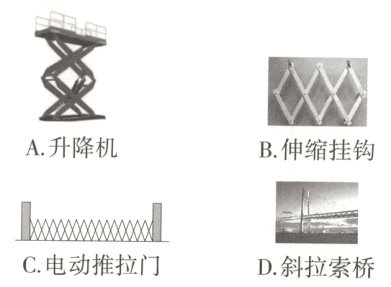
A. 升降机
B. 伸缩挂钩
C. 电动推拉门
D. 斜拉索桥

答案： D 升降机，伸缩挂钩，电动推拉门都是利用了四边形的不稳定性，斜拉索桥利用了三角形的稳定性.故选D.

10. (2024四川遂宁中考,6,)佩佩在“黄娥古镇”研学时学习扎染技术,得到一个内角和为1080°的正多边形图案，这个正多边形的每个外角为(M8215001)( )
A. 36°
B. 40°
C. 45°
D. 60°

答案： C 设这个正多边形的边数为n，
由题意得(n - 2)·180° = 1 080°，
解得n = 8，
∵360°÷8 = 45°，
∴这个正多边形的每个外角为45°.故选C.

11. (2024北京朝阳月考,3,)正十边形的内角和是下列哪个图形内角和的2倍( )

答案： C 正十边形的内角和是(10 - 2)×180° = 1 440°，1 440°÷2 = 720°.A选项中图形的内角和为(4 - 2)×180° = 360°，不符合题意；
B选项中图形的内角和为(5 - 2)×180° = 540°，不符合题意；
C选项中图形的内角和为(6 - 2)×180° = 720°，符合题意；
D选项中图形的内角和为(7 - 2)×180° = 900°，不符合题意.故选C.

12. (2023北京海淀中关村中学质检,5,)如图,一只蚂蚁从点A出发,每向前爬行5厘米,就向左边偏转9°,当这只蚂蚁回到点A时,共爬行了(M8215001)( )

A. 100厘米
B. 200厘米
C. 400厘米
D. 不能回到点A

答案： B 360°÷9°×5 = 40×5 = 200(厘米).故选B.

13. (2024北京八中月考,11,)如图所示的是由射线AB,BC,CD,DE,EF,FA组成的平面图形,则∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = _______°.

答案： 答案 360
解析
∵任意多边形的外角和是360°，
∴∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 360°.

14. (2024北京通州期中,12,)如图,∠1、∠2、∠3是五边形ABCDE的三个外角,延长EA、CB交于点O.如果∠1 + ∠2 + ∠3 = 240°,那么∠AOB的度数为_______.

答案： 答案 60°
解析
∵多边形的外角和等于360°，
∴∠1 + ∠2 + ∠3 + ∠OAB + ∠OBA = 360°，
∵∠1 + ∠2 + ∠3 = 240°，
∴∠OAB + ∠OBA = 120°，
∴∠AOB = 180° - 120° = 60°.

15. (2023吉林长春中考,13,)如图,将正五边形纸片ABCDE折叠,使点B与点E重合,折痕为AM,展开后,再将纸片折叠,使边AB落在线段AM上,点B的对应点为点B',折痕为AF,则∠AFB'的大小为_______度.

答案： 答案 45
解析
∵正五边形ABCDE的内角和为(5 - 2)×180° = 540°，
∴∠B = ∠BAE = 540°÷5 = 108°，由折叠可知∠BAM = ∠EAM，∠BAF = ∠B'AF，∠AFB = ∠AFB'，
∴∠BAM = ∠EAM = $\frac{1}{2}$∠BAE = 54°，
∴∠BAF = ∠FAB' = $\frac{1}{2}$∠BAM = 27°，
∴∠AFB' = ∠AFB = 180° - ∠B - ∠BAF = 180° - 108° - 27° = 45°.

16. 新考向·规律探究题(2023湖南常德澧县三模,16,)图1被称为二环三角形,它的内角和等于∠A + ∠B + ∠C + ∠A₁ + ∠B₁ + ∠C₁;图2被称为二环四边形,它的内角和等于∠A + ∠B + ∠C + ∠D + ∠A₁ + ∠B₁ + ∠C₁ + ∠D₁; ……,依此规律,可知二环n边形的内角和为____________度.(用含n的式子表示,n ≥ 3)

答案：
答案 360(n - 2)
解析 如图，连接BB₁，
∵∠1 + ∠2 = ∠A₁ + ∠C，

∵四边形ABB₁C₁的内角和为360°，
∴二环三角形的内角和为360°.
如图，连接AA₁，B₁D₁，

同理可得二环四边形的内角和=(5 - 2)×180° + 180° = 2×360°，……，
∴二环n边形的内角和为360(n - 2)度.