《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

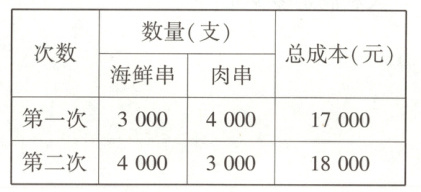
5. (2023湖北襄阳中考)在襄阳市创建“经济品牌特色品牌”政策的影响下.每到傍晚,市内某烧烤店就食客如云,这家烧烤店的海鲜串和肉串非常畅销,店主从食品加工厂批发以上两种产品进行加工销售,其中海鲜串的成本为m元/支,肉串的成本为n元/支.两次购进并加工海鲜串和肉串的数量与成本如下表所示(成本包括进价和其他费用):

针对团体消费,店主决定每次消费海鲜串不超过200支时,每支售价5元;超过200支时,不超过200支的部分按原价,超过200支的部分打八折.每支肉串的售价为3.5元.(M8214006)
(1)求m、n的值.
(2)五一当天,一个旅游团去此店吃烧烤,一次性消费海鲜串和肉串共1 000支,且海鲜串不超过400支.在本次消费中,设该旅游团消费海鲜串x支,店主获得海鲜串的总利润为y元,求y与x的函数关系式,并写出自变量x的取值范围.
(3)在(2)的条件下,该旅游团消费的海鲜串超过了200支,店主决定给该旅游团更多优惠,对每支肉串降价a(0 ＜ a ＜ 1)元,但要确保本次消费获得肉串的总利润始终不低于海鲜串的总利润,求a的最大值.

答案： 解析　
(1)根据表格可得$\begin{cases}3000m + 4000n = 17000\\4000m + 3000n = 18000\end{cases}$，解得$\begin{cases}m = 3\\n = 2\end{cases}$.
(2)当0＜x≤200时，y = (5 - 3)x = 2x；
当200＜x≤400时，y = (5 - 3)×200+(5×0.8 - 3)(x - 200)=x + 200.
∴y = $\begin{cases}2x(0＜x≤200)\\x + 200(200＜x≤400)\end{cases}$.
(3)设降价后获得肉串的总利润为z元，令W = z - y.
∵200＜x≤400，
∴z = (3.5 - a - 2)(1000 - x)=(a - 1.5)x + 1500 - 1000a，
∴W = z - y=(a - 2.5)x + 1300 - 1000a，
∵0＜a＜1，
∴a - 2.5＜0，
∴W随x的增大而减小，当x = 400时，W最小，由题意可得z≥y，
∴W≥0，
即(a - 2.5)×400 + 1300 - 1000a≥0，
解得a≤0.5，
∴a的最大值是0.5.

6. (2024北京海淀首都师大附中模拟,8,★★☆)如图①,底面积为30 cm²的空圆柱容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②,若“几何体”的下方圆柱的底面积为15 cm²,则“几何体”上方圆柱体的底面积为（ ）

A. 24 cm²
B. 12 cm²
C. 18 cm²
D. 21 cm²

答案： 6A根据函数图象得圆柱形容器的高为14cm，两个实心圆柱组成的“几何体”的高度为11cm，水从刚没过由两个实心圆柱组成的“几何体”到注满用了42 - 24 = 18(s)，这段高度为14 - 11 = 3(cm)，设匀速注水的水流速度为x cm³/s，则18·x = 30×3，解得x = 5，即匀速注水的水流速度为5 cm³/s.由函数图象得“几何体”下方圆柱的高为a cm，则(30 - 15)a = 18×5，解得a = 6，
∴“几何体”上方圆柱的高为11 - 6 = 5(cm)，设“几何体”上方圆柱的底面积为S cm²，根据题意得5(30 - S)=5×(24 - 18)，解得S = 24，
∴“几何体”上方圆柱体的底面积为24 cm².

7. (2024陕西中考A卷,22,★★☆)我国新能源汽车快速健康发展,续航里程不断提升,王师傅驾驶一辆纯电动汽车从A市前往B市,他驾车从A市一高速公路入口驶入时,该车的剩余电量是80 kW·h,行驶了240 km后,从B市一高速公路出口驶出.已知该车在高速公路上行驶的过程中,剩余电量y(kW·h)与行驶路程x(km)之间的关系如图所示.
(1)求y与x之间的关系式;
(2)已知这辆车的“满电量”为100 kW·h,求王师傅驾车从B市这一高速公路出口驶出时,该车的剩余电量占“满电量”的百分之多少.

答案： 解析　
(1)设y = kx + b(0≤x≤240)，
将(0,80)，(150,50)代入，
得$\begin{cases}b = 80\\150k + b = 50\end{cases}$，解得$\begin{cases}k = -\frac{1}{5}\\b = 80\end{cases}$，
∴y = -$\frac{1}{5}$x + 80.
(2)令x = 240，则y = 32，
$\frac{32}{100}$×100% = 32%.
答：该车的剩余电量占“满电量”的32%.