《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

9.跨物理·密度 铁的密度约为7.9 kg/m³,铁的质量m(kg)与体积V(m³)成正比.一个体积为10 m³的铁块,它的质量为______kg.

答案： 由题意得m = 7.9V，
∴当V = 10 m³时，m = 10×7.9 = 79(kg).

10.(2024北京五中期中)已知点P(x,y),其中xy＜0,且它到x轴的距离为2,到y轴的距离为3,请写出点P的坐标:__________.

答案：
∵xy ＜ 0，
∴x，y异号，
∵点P(x,y)到x轴的距离为2，到y轴的距离为3，
∴P(3,-2)或(-3,2).

11.(2024北京五十七中期中)我们规定:在平面直角坐标系xOy中,任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1 - x2|+|y1 - y2|,例如,图①中,点M(-2,3)与点N(1,-1)之间的折线距离为d(M,N)=|-2 - 1|+|3 - (-1)|=3 + 4 = 7.如图②,已知点P(3,-4),若点Q的坐标为(t,2),且d(P,Q)=10,则t的值为______.

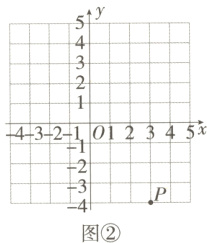
答案：
∵P(3,-4)，Q(t,2)，且d(P,Q) = 10，
∴|3 - t| + | - 4 - 2| = 10，解得t = -1或t = 7.

12.如图,四边形OABC是边长为1的正方形,顶点A在x轴的负半轴上,顶点C在y轴的正半轴上,若直线y = kx + 2与边AB有公共点,则k的取值范围是______.

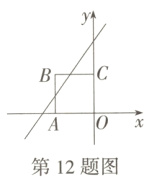
答案： 由题意可得点A(-1,0)，点B(-1,1)，把A(-1,0)代入y = kx + 2得-k + 2 = 0，解得k = 2，把B(-1,1)代入y = kx + 2得-k + 2 = 1，解得k = 1，所以k的取值范围为1≤k≤2.

13.情境题·中华优秀传统文化 (2024北京一〇一中学期中)漏刻是我国古代的一种计时工具,这是中国古代人民对函数思想的创造性应用.小明同学依据漏刻的原理制作了一个简单的漏刻计时模型,研究中发现水位h(cm)是时间t(min)的一次函数,下表是小明记录的部分数据,当t = 4时,h的值为______.

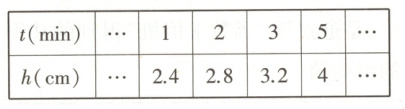
答案： 由题意知h是t的一次函数，设h = kt + b(k≠0)，把(1,2.4)，(2,2.8)代入得$\begin{cases}k + b = 2.4\\2k + b = 2.8\end{cases}$，解得$\begin{cases}k = 0.4\\b = 2\end{cases}$，
∴h = 0.4t + 2，当t = 4时，h = 0.4×4 + 2 = 3.6.

14.(2024山东青岛崂山期末)一次函数y = ax + b与y = mx + n的图象如图所示,下列说法:①am＜0;②bn＜0;③两个函数都是y随x的增大而减小;④ax + b＞mx + n的解集为x＞-3;⑤3(m - a)=n - b.其中正确的是__________(请填写序号).

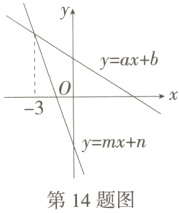
答案：
∵一次函数y = ax + b的图象经过第一、二、四象限，
∴a ＜ 0，b ＞ 0，
∵一次函数y = mx + n的图象经过第二、三、四象限，
∴m ＜ 0，n ＜ 0，
∴am ＞ 0，故①错误；bn ＜ 0，故②正确；两个函数都是y随x的增大而减小，故③正确；
∵一次函数y = ax + b与y = mx + n的图象交点坐标的横坐标为-3，
∴ax + b ＞ mx + n的解集为x ＞ -3，故④正确；易得-3a + b = -3m + n，
∴3(m - a) = n - b，故⑤正确. 故正确的是②③④⑤.

15.(6分)我们定义:关于x的一次函数y = ax + b与y = bx + a叫做一对交换函数,例如y = 3x + 4与y = 4x + 3就是一对交换函数.
(1)写出一次函数y = -2x + b的交换函数:__________.
(2)当b≠-2时,写出(1)中两函数图象的交点的横坐标:_____.
(3)如果(1)中两函数图象与y轴围成的三角形的面积为3,求b的值.

答案：
(1)一次函数y = -2x + b的交换函数为y = bx - 2.
(2)将y = -2x + b代入y = bx - 2，得-2x + b = bx - 2，整理得(b + 2)x = b + 2，
∵b≠ - 2，
∴x = 1，
∴两函数图象的交点的横坐标为1.
(3)设函数y = -2x + b的图象与y轴的交点为A，函数y = bx - 2的图象与y轴的交点为B，则A点的坐标为(0,b)，B点的坐标为(0,-2).
∵两函数图象与y轴围成的三角形的面积为3，交点到y轴的距离为1，
∴$\frac{1}{2}$AB×1 = 3，
∴AB = 6，
∴b - (-2) = 6或-2 - b = 6，
∴b = 4或b = -8.