《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

1. 新独家原创 情境题·中华优秀传统文化 下列剪纸图案中既是轴对称图形又是中心对称图形的是(M8215005) ( )

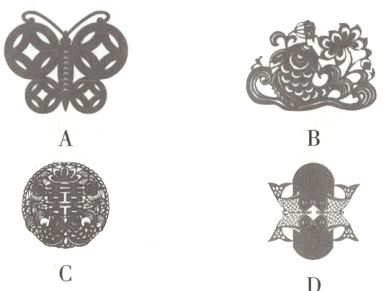
答案： A.是轴对称图形,不是中心对称图形;B.既不是轴对称图形也不是中心对称图形;C.是轴对称图形,不是中心对称图形;D.既是轴对称图形又是中心对称图形.故选D.

2.(2024吉林长春中考)在剪纸活动中，小花同学想用一张矩形纸片剪出一个正五边形，其中正五边形的一条边与矩形的边重合，如图所示，则∠α的大小为(M8215001) ( )

A.54°　　
　B.60°　　
　C.70°　　
　D.72°

答案： $\angle\alpha = 180^{\circ}-\frac{(5 - 2)\times180^{\circ}}{5}=72^{\circ}$.故选D.

3. 情境题·中华优秀传统文化 (2024北京海淀清华附中期中)小雨在参观故宫博物院时，被太和殿窗棂(如图1所示)的“三交六椀”菱花图案所吸引，他从中提取出一个含60°角的菱形ABCD(如图2所示).若AB的长度为a，则菱形ABCD的面积为(M8215002) ( )
　　
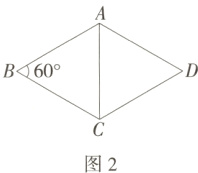
A.$\frac{\sqrt{3}}{4}$a²　　
　B.$\sqrt{3}$a²　
　C.a²　　　
　D.$\sqrt{3}$a²

答案：
过A作$AH\perp BC$于H,如图，
　　　　　　　　
　
∵四边形ABCD是菱形，
∴$AB = BC = a$，
　
∵$\angle B = 60^{\circ}$，
∴$\triangle ABC$是等边三角形，
　
∵$AH\perp BC$，
∴$\angle BAH = 90^{\circ}-\angle B = 30^{\circ}$，
　
∴$BH=\frac{1}{2}AB=\frac{1}{2}a$，
　　在$Rt\triangle ABH$中，$AH = \sqrt{AB^{2}-BH^{2}}=\frac{\sqrt{3}}{2}a$，
　
∴菱形ABCD的面积 = $BC\cdot AH=\frac{\sqrt{3}}{2}a^{2}$.故选B.

4. 新考向·新定义试题 (2024河北中考)在平面直角坐标系中，我们把一个点的纵坐标与横坐标的比值称为该点的“特征值”.如图，矩形ABCD位于第一象限，其四条边分别与坐标轴平行，则该矩形四个顶点中“特征值”最小的是 ( )
　　　
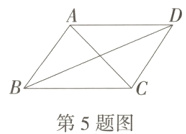
A.点A　　
　B.点B　　
　C.点C　
　D.点D

答案： 由题意得点A、B、C、D的横、纵坐标均为正数.
∵点A和点D的横坐标相同,点D的纵坐标大于点A的纵坐标,
∴点A的“特征值”小于点D的“特征值”.同理，点B的“特征值”小于点C的“特征值”.
∵点A和点B的纵坐标相同，点B的横坐标大于点A的横坐标，
∴点B的“特征值”小于点A的“特征值”,
∴该矩形四个顶点中“特征值”最小的是点B.故选B.

5. 新独家原创 如图，从下列五个条件中任选三个，使四边形ABCD是正方形，可以选择的组合有 ( )
①AB//CD，AB = CD；②∠ABC = 90°；③AC⊥BD；④AC = BD；⑤AB = BC.
A.2种　　
　B.3种　　
　C.4种　　
　D.5种

答案： 可以选择的组合有①②③；①②⑤；①③④；①④⑤，共4种.故选C.

6.(2024甘肃临夏州中考)如图，O是坐标原点，菱形ABOC的顶点B在x轴的负半轴上，顶点C的坐标为(3，4)，则顶点A的坐标为 ( )

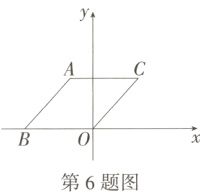
A.(−4,2)　　　　　　
　B.($\sqrt{3}$,4)
C.(−2,4)　　　　　　
　D.(−4,$\sqrt{3}$)

答案：
过C作$CN\perp x$轴于N,过A作$AM\perp x$轴于M,如图，
　　　　　　　　
　
∵点C的坐标为(3,4)，
∴$ON = 3$，$CN = 4$，
　
∴$OC=\sqrt{ON^{2}+CN^{2}} = 5$，
　
∵四边形ABOC是菱形，
∴$AC = OC = 5$，$AC// BO$，
　
∵$CN\perp MN$，$AM\perp MN$，
　
∴$\angle AMN=\angle MNC=\angle ACN = 90^{\circ}$，
　
∴四边形AMNC是矩形，
∴$MN = AC = 5$，
　
∴$OM = MN - ON = 2$，
　
∴点A的坐标为(-2,4).故选C.

7.(2024四川自贡中考)如图，在□ABCD中，∠B = 60°，AB = 6 cm，BC = 12 cm.点P从点A出发，以1 cm/s的速度沿A→D运动，同时点Q从点C出发，以3 cm/s的速度沿C→B→C→…往复运动，当点P到达点D时，点Q随之停止运动.在此运动过程中，线段PQ = CD出现的次数是 ( )

A.3　　　
　B.4　　　
　C.5　　　
　D.6

答案：
在$\square ABCD$中，$AB = 6\ cm$，$BC = 12\ cm$，
　
∴$CD = AB = 6\ cm$，$AD = BC = 12\ cm$，$AD// BC$，
　
∵点P从点A出发，以1 cm/s的速度沿$A\rightarrow D$运动，
　
∴点P从点A出发，到达点D的时间为$12\div1 = 12(s)$，
　
∵点Q从点C出发，以3 cm/s的速度沿$C\rightarrow B\rightarrow C\rightarrow\cdots$往复运动，
　
∴点Q从点C出发，第一次到点B的时间为$12\div3 = 4(s)$，
　　第一次返回到点C的时间为$24\div3 = 8(s)$，第二次到点B的时间为$36\div3 = 12(s)$.
　　设P，Q同时运动的时间为$t(s)$，
　　当$0\lt t\leq4$时，
　　当$DP = CQ$时，四边形CDPQ为平行四边形，
　
∴$PQ = CD$，此时$12 - t = 3t$，
∴$t = 3$.
　　当$PQ = AB$且PQ与AB不平行时，四边形CDPQ为等腰梯形，
∴$PQ = AB = CD$.
　　如图，过点A，P分别作BC的垂线，分别交BC于点M，N，
　　　　　　　
　
∴四边形AMNP是矩形，
∴$MN = AP = t$，$AM = PN$，
　
∵四边形ABQP是等腰梯形，
　
∴$PQ = AB$，$\angle PQN=\angle B$，
　
∵$\angle BAM = 90^{\circ}-\angle B$，$\angle QPN = 90^{\circ}-\angle PQN$，
　
∴$\angle BAM=\angle QPN$，在$\triangle ABM$和$\triangle PQN$中，
　　$\begin{cases}AM = PN\\\angle BAM=\angle QPN\\AB = PQ\end{cases}$，
∴$\triangle ABM\cong\triangle PQN$，
　
∴$BM = QN$，
　　在$Rt\triangle ABM$中，$\angle B = 60^{\circ}$，$AB = 6\ cm$，
　
∴$\angle BAM = 90^{\circ}-\angle B = 30^{\circ}$，
　
∴$BM=\frac{1}{2}AB = 3\ cm$，
∴$QN = BM = 3\ cm$，
　
∴$t = 12 - 3t - 3 - 3$，
∴$t=\frac{3}{2}$.
　　当$4\lt t\leq8$时，当$DP = CQ$时，四边形CDPQ为平行四边形，
∴$PQ = CD$，此时$12 - t = 12 - 3(t - 4)$，
∴$t = 6$.
　　当$PQ = AB$且PQ与AB不平行时，四边形CDPQ为等腰梯形，易知此时$PD＞6\ cm$，
　
∴这种情况在$4\lt t\leq8$时不存在.
　　当$8\lt t\leq12$时，当$DP = CQ$时，四边形CDPQ为平行四边形，
∴$PQ = CD$，此时$12 - t = 3(t - 8)$，
∴$t = 9$.
　　综上，当$t=\frac{3}{2}$或$t = 3$或$t = 6$或$t = 9$时，$PQ = CD$，共出现4次.故选B.