《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

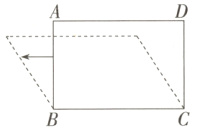
8. (2023湖北十堰中考,5,★☆☆)如图，将四根木条用钉子钉成一个矩形框架ABCD，然后向左扭动框架，观察所得四边形的变化，下面判断错误的是（ ）　　　　　　　　　　　　　　
A. 四边形ABCD由矩形变为平行四边形
B. 对角线BD的长度减小
C. 四边形ABCD的面积不变
D. 四边形ABCD的周长不变
　　　　　　　　　　　　　　　　

答案： C 向左扭动矩形框架ABCD，只改变四边形的形状，矩形变成平行四边形，A不符合题意；此时对角线BD的长度减小，对角线AC的长度增大，B不符合题意；BC边上的高减小，故面积变小，C符合题意；四边形的四条边的长度不变，故周长不变，D不符合题意.故选C.

9. (2023广东深圳中考改编,5,★☆☆)如图，在平行四边形ABCD中，CD = 4，BC = 6，将线段AB水平向右平移a个单位长度得到线段FE，若四边形ECDF为菱形，则a的值为（ ）
A. 1　　　　B. 2　　　　C. 3　　　　D. 4
　　　　　　　　　　　　　　　　

答案： B
∵四边形ABCD是平行四边形，
∴AB//CD，CE//FD，
∵将线段AB水平向右平移得到线段FE，
∴AB//EF//CD，
∴四边形ECDF为平行四边形，当CD = CE = 4时，□ECDF为菱形，此时a = 6 - 4 = 2.故选B.

10. (2024北京延庆期末改编,8,★★☆)学习了正方形之后，老师提出问题：要判定一个四边形是正方形，有哪些思路？
　甲同学说：“先判定四边形是菱形，再确定这个菱形有一个角是直角。”
　乙同学说：“先判定四边形是矩形，再确定这个矩形有一组邻边相等。”
　丙同学说：“先判定四边形是平行四边形，再确定这个平行四边形有一个角是直角并且有一组邻边相等。”
　上述三名同学的说法中，正确的是（ ）
A. 甲、乙　　　　　　　B. 甲、丙
C. 乙、丙　　　　　　　D. 甲、乙、丙

答案： D 正方形是有一个角是直角的菱形，故甲同学说法正确；正方形是有一组邻边相等的矩形，故乙同学说法正确；正方形是有一个角是直角并且有一组邻边相等的平行四边形，故丙同学说法正确.故选D.

11. (2022湖南邵阳中考,17,★★☆)如图，在等腰△ABC中，∠A = 120°，顶点B在□ODEF的边DE上，已知∠1 = 40°，则∠2 =________。
　　　　　

答案： 答案 110°
解析
∵在等腰△ABC中，∠A = 120°，
∴∠ABC = 30°，
∵∠1 = 40°，
∴∠ABE = ∠1+∠ABC = 70°，
∵四边形ODEF是平行四边形，
∴OF//DE，
∴∠2 = 180° - ∠ABE = 180° - 70° = 110°.

12. (2024湖北恩施州模拟,17,★★☆)已知：如图，在Rt△ABC中，∠ACB = 90°，CD是△ABC的角平分线，DE⊥BC，DF⊥AC，垂足分别为点E，F，求证：四边形CEDF是正方形。

答案： 证明
∵∠ACB = 90°，DE⊥BC，DF⊥AC，
∴DE//FC，DF//CE，
∴四边形DECF是平行四边形，
∵∠ACB = 90°，
∴四边形DECF是矩形，
∵CD平分∠ACB，DE⊥BC，DF⊥AC，
∴DE = DF，
∴四边形DECF是正方形.

13. 函数思想 (2024北京石景山期末,20,★★☆)工艺美术中常需要设计几何图案。如图，在5×5的正方形网格中，已确定三个格点A，B，C的位置，需要在图中确定点P，使得以P，A，B，C为顶点的四边形为平行四边形。为了精准刻画点P的位置，需建立平面直角坐标系xOy。若点A(2,2)，C(3,1)。
(1) 请画出平面直角坐标系xOy。
(2) 在图中描出点P的位置，并写出所有符合条件的点P的坐标。

答案：
解析
(1)建立的平面直角坐标系xOy如图.

(2)如图，所有符合条件的点P的坐标为(0，1)，(2，-1)，(4，3).