《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

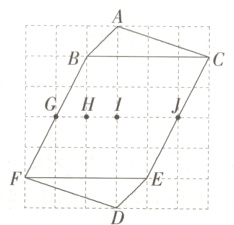
7.（2023北京大兴一模改编,7,★☆☆）如图，在正方形网格中，A，B，C，D，E，F，G，H，I，J是网格线交点，由△ABC、△DEF和平行四边形BCEF组成的图形是中心对称图形，则这个图形的对称中心是（ ）

A.点G
B.点H
C.点I
D.点J

答案：
如图，
∵ 四边形 BCEF 是平行四边形，
∴ 对角线 BE 和 CF 的交点 I 是对称中心.故选 C.

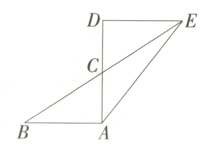
8.（2024北京师大附中期末,15,★☆☆）如图，△DEC与△ABC关于点C成中心对称，AB = 3，AC = 2，∠CAB = 90°，则AE的长是________.(M8215005)

答案： 答案 5
解析 由题意得△DEC≌△ABC，
∴DC = AC = 2，∠D = ∠BAC = 90°，DE = AB = 3，
∴AD = 4，
∴AE = $\sqrt{DE^{2}+AD^{2}}=\sqrt{3^{2}+4^{2}} = 5$.

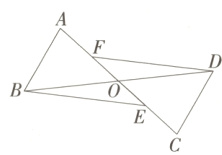
9.（2023北京和平街一中期中,19,★☆☆）如图，△ABO与△CDO关于点O成中心对称，点E，F在线段AC上，且AF = CE，求证：FD = BE.(M8215005)

答案： 证明
∵△ABO 与△CDO 关于点 O 成中心对称，
∴BO = DO，AO = CO，
∵AF = CE，
∴AO - AF = CO - CE，
∴FO = EO，
在△FOD 和△EOB 中，
$\begin{cases}FO = EO,\\\angle FOD=\angle EOB,\\DO = BO,\end{cases}$
∴△FOD≌△EOB(SAS)，
∴DF = BE.

10. 抽象能力（2024浙江宁波慈溪期中）如图，由4个全等的正方形组成的“L”形图案，请按下列要求画图：
(1)在图案①中添加1个正方形，使它成为轴对称图形（不能是中心对称图形）.
(2)在图案②中添加1个正方形，使它成为中心对称图形（不能是轴对称图形）.
(3)在图案③中改变1个正方形的位置，得到一个新图形，使它既是中心对称图形，又是轴对称图形.

答案：
解析
(1)如图 1，图 2，图 3 所示.
(2)如图 4 所示.
(3)如图 5，图 6 所示.

11. 推理能力 已知：如图所示，△ABC为任意三角形，若将△ABC绕点C顺时针旋转180°得到△DEC，连接AE，BD.
(1)试猜想AE与BD的关系，并直接写出答案.
(2)若△ABC的面积为3 cm²，求四边形ABDE的面积.
(3)请给△ABC添加条件，使旋转得到的四边形ABDE为菱形，并说明理由.

答案： 解析
(1)AE = BD，AE//BD.详解：由旋转的性质可知，CA = CD，CB = CE，
∴ 四边形 ABDE 是平行四边形，
∴AE = BD，AE//BD.
(2)
∵ 四边形 ABDE 是平行四边形，
∴△BCD 的面积 = △DCE 的面积 = △AEC 的面积 = △ABC 的面积 = 3 $cm^{2}$，
∴ 四边形 ABDE 的面积为 12 $cm^{2}$.
(3)∠ACB = 90°.
理由：
∵∠ACB = 90°，
∴AD⊥BE，
∵ 四边形 ABDE 是平行四边形，
∴ 四边形 ABDE 为菱形.(答案不唯一)