《2025年5年中考3年模拟八年级数学下册北京课改版北京专版》

5.(2024山东青岛期末)一张矩形纸片ABCD，将点B翻折到对角线AC上的点M处，折痕CE交AB于点E。将点D翻折到对角线AC上的点H处，折痕AF交DC于点F，折叠出四边形AECF，如图。
(1)求证：AF//CE。
(2)当∠BAC为多少度时，四边形AECF是菱形？请说明理由。
　　　　　　　　　　　　

答案： 解析
(1)证明：
∵ 四边形ABCD是矩形，
∴ AD//BC，
∴ ∠DAC = ∠BCA，
由翻折的性质得∠DAF = ∠HAF = $\frac{1}{2}∠DAC$，∠BCE = ∠MCE = $\frac{1}{2}∠BCA$，
∴ ∠HAF = ∠MCE，
∴ AF//CE.
(2)当∠BAC = 30°时，四边形AECF为菱形，理由如下：
∵ 四边形ABCD是矩形，
∴ ∠D = ∠BAD = 90°，AB//CD，
由
(1)得AF//CE，
∴ 四边形AECF是平行四边形，
∵ ∠BAC = 30°，
∴ ∠DAC = 60°，∠ACD = 30°，
∴ ∠DAF = ∠HAF = 30°，
∴ ∠HAF = ∠ACD，
∴ AF = CF，
∴ 四边形AECF是菱形.

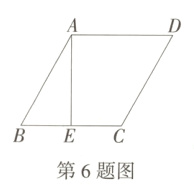
6.(2024福建厦门海沧期末)如图，在菱形ABCD中，E是边BC上一点，连接AE。将菱形沿AE折叠，点B恰与点C重合。若菱形的边长为4，则AE的长是 ( )
　
A.2
B.4
C.2√3
D.4√3

答案： C
∵ 四边形ABCD是菱形，
∴ AB = BC = 4，
由折叠的性质得BE = EC = 2，AE⊥BC，
∴ AE = $\sqrt{AB^{2}-BE^{2}} = 2\sqrt{3}$.故选C.

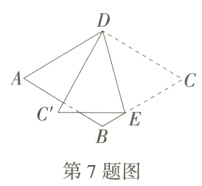
7.(2023广西贵港四模)如图，在菱形纸片ABCD中，∠A = 60°，点E在BC上，将菱形纸片ABCD沿DE折叠，点C对应点为C'，且DC'是AB的垂直平分线，则∠DEC的大小为 ( )
　　
A.30°
B.45°
C.60°
D.75°

答案：
D 如图，连接BD，令DC'与AB交于点P，

∵ 四边形ABCD为菱形，
∴ AB = AD，
∵ ∠A = 60°，
∴ △ABD为等边三角形，∠ADC = 120°，∠C = 60°，
∵ DC'是AB的垂直平分线，
∴ P为AB的中点，
∴ DP为∠ADB的平分线，
∴ ∠ADP = ∠BDP = 30°，
∴ ∠PDC = 90°，
∴ ∠CDE = ∠PDE = 45°，
在△DEC中，∠DEC = 180° - 45° - 60° = 75°.故选D.

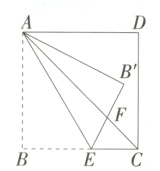
8.(2024陕西西安临潼期末)如图，在正方形ABCD中，E为边BC上一点，将△ABE沿AE折叠至△AB'E处，B'E与AC交于点F，若∠EFC = 69°，则∠CAE的大小为 ( )
　
A.10°
B.12°
C.14°
D.15°

答案： B
∵ ∠EFC = 69°，∠ACE = 45°，
∴ ∠BEF = 69° + 45° = 114°，
由折叠的性质得∠BEA = $\frac{1}{2}∠BEF = 57°$，
∴ ∠BAE = 90° - 57° = 33°，
∴ ∠EAC = 45° - 33° = 12°.故选B.

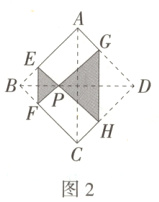
9.(2024贵州毕节织金一模)如图1，将正方形纸片ABCD的∠ABC和∠ADC进行折叠，使两个直角顶点重合于对角线BD上的点P处，如图2，EF、GH分别是折痕，若点P沿BD从点B向点D移动，则阴影部分的周长 ( )
　　　
A.先变大，后变小
B.先变小，后变大
C.当点P在BD中点处时，阴影部分周长最大
D.保持不变

答案： D 由折叠的性质得△BEF≌△PEF，△DGH≌△PGH，
∴ EP = EB，FP = FB，∠EPF = ∠EBF = ∠GPH = ∠GDH = 90°，
易得点E，点P，点H在同一条直线上，点F，点P，点G在同一条直线上，
∴ ∠EPG = ∠FPH = 90°，
∵ 两个直角顶点重合于对角线BD上的点P处，
∴ EF是BP的垂直平分线，GH是PD的垂直平分线，
∵ AC与BD互相垂直平分，
∴ EF//AC//GH，
∴ ∠BEF = ∠BAC = 45°，
∴ ∠BEP = 90°，
∴ 四边形BEPF是矩形，
∴ EF = BP，
同理可得GH = PD，
∵ ∠AEP = ∠EPG = ∠EAG = 90°，
∴ 四边形AEPG是矩形，
∴ AE = PG，
同理可得FC = PH，
∴ 阴影部分的周长 = EP + PG + GH + HP + PF + FE = BE + AE + PD + FC + BF + BP = AB + BC + BD，
∴ 阴影部分的周长保持不变.故选D.

10.半角模型 如图，在正方形ABCD中，AB = 12，E是AD边上的一点，将正方形沿CE折叠，点D的对应点为点F，点G为AB的中点，当点F恰好落在线段EG上时。求证：
(1)∠ECG = 45°。
(2)AF//CG。

答案： 证明
(1)由折叠的性质得CD = CF，
∵ 四边形ABCD是正方形，
∴ CB = CD = CF，
在Rt△BCG和Rt△FCG中，$\begin{cases}CG = CG \\ CB = CF\end{cases}$，
∴ Rt△BCG≌Rt△FCG(HL)，
∴ ∠BCG = ∠FCG，
又
∵ ∠FCE = ∠DCE，
∴ ∠ECG = ∠FCG + ∠FCE = $\frac{1}{2}∠BCD = 45°$.
(2)由
(1)得Rt△BCG≌Rt△FCG，
∴ GF = BG = AG，∠CGF = ∠CGB，
∴ ∠GAF = ∠GFA，
∵ ∠BGF = ∠CGF + ∠CGB = ∠GAF + ∠GFA，
∴ ∠CGF = ∠CGB = ∠GAF = ∠GFA，
∴ AF//CG.